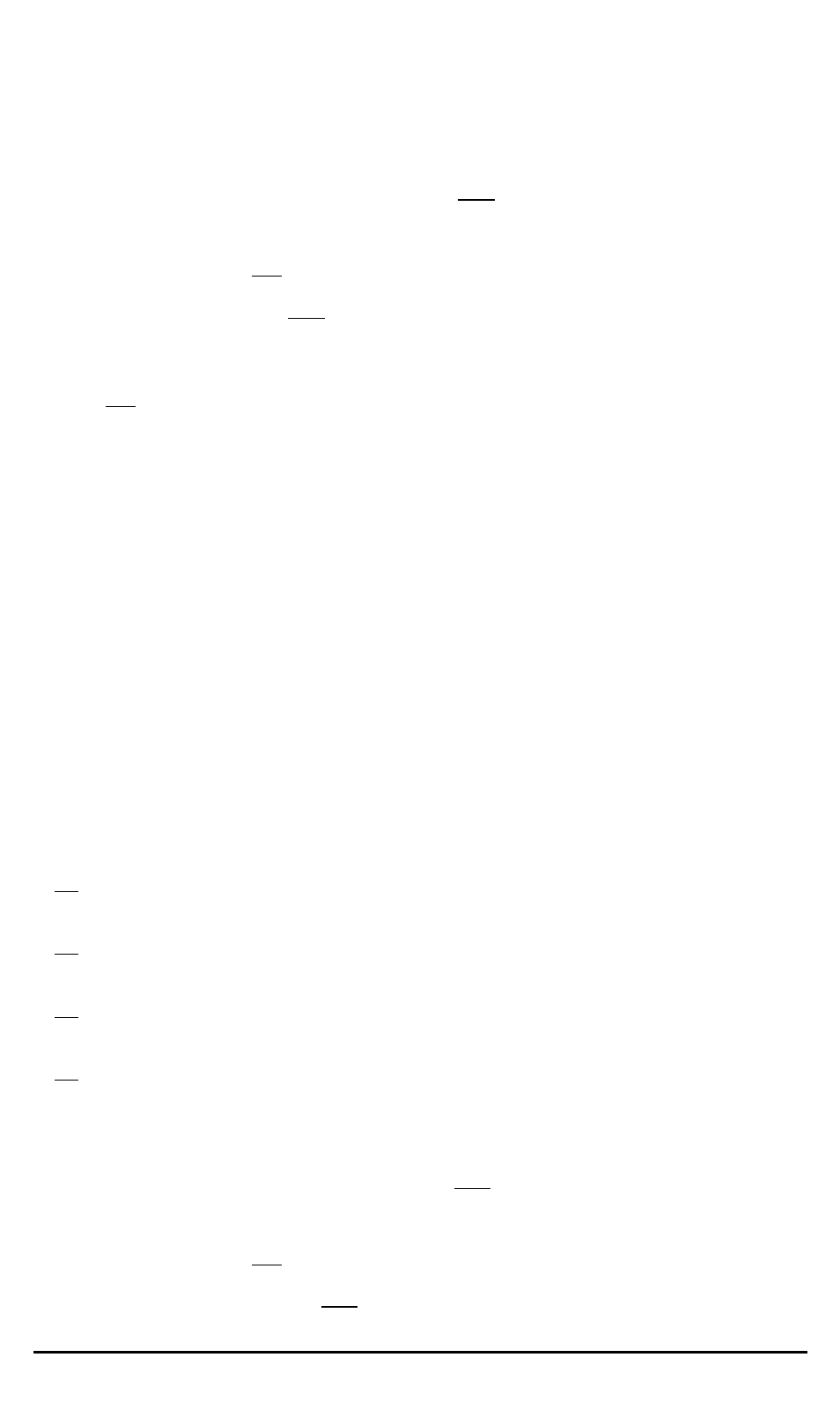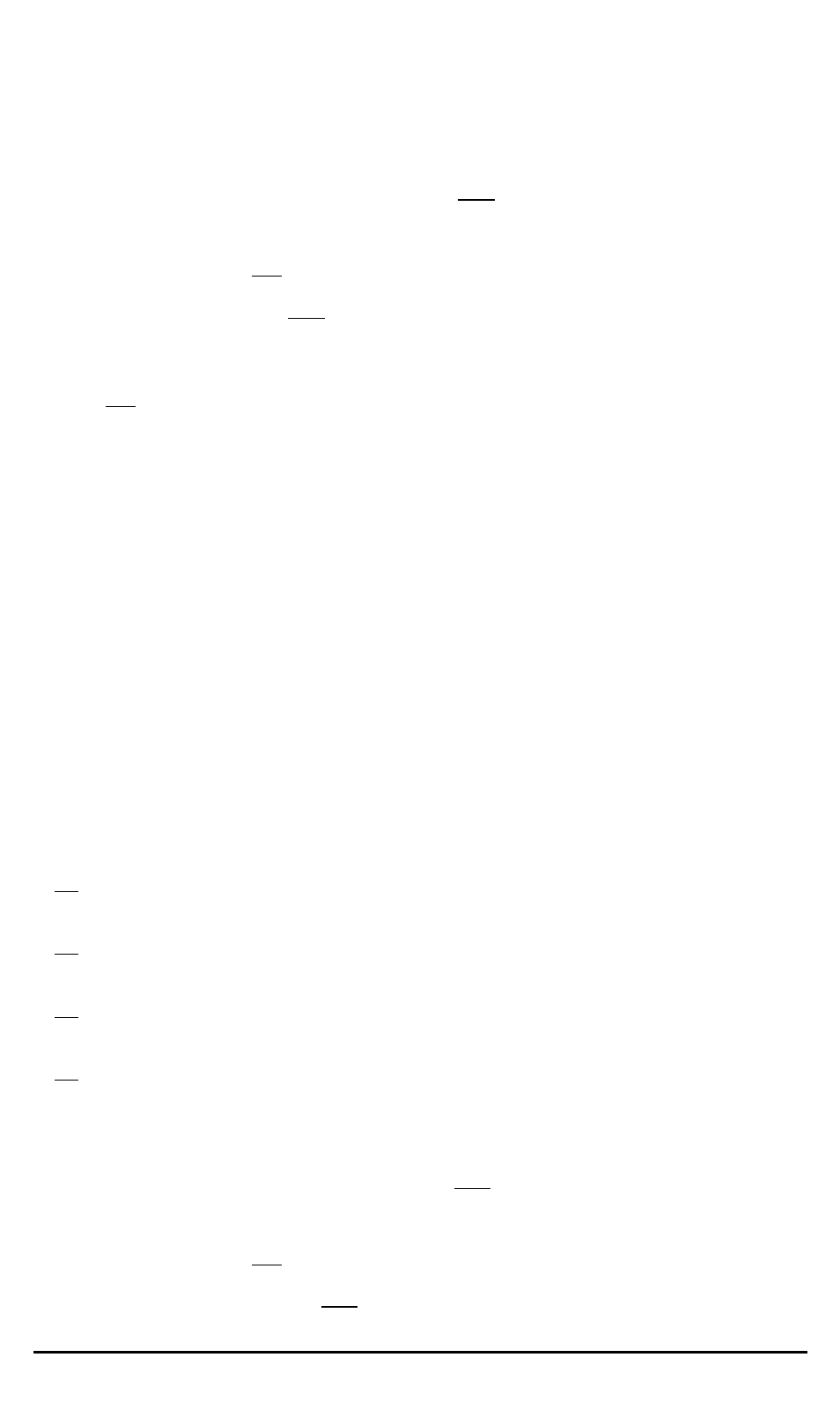
Дляоднозначного определенияфункций
n
k
заданы следующие
дополнительные условия, соответствующие рассматриваемой физиче-
ской ситуации:
n
1
(
x, t
0
) =
n
1
,
0
(
x
)
, x
∈
Q,
n
k
(
x, t
0
) = 0
, k
= 2
,
6
, x
∈
Q,
α
k
(
x, t
)
∂
∂n
n
k
(
x, t
) +
β
k
(
x, t
)
n
k
(
x, t
) =
r
k
(
x, t
)
,
k
= 1
,
6
, x
∈
∂Q, t
∈
(
t
0
, t
1
)
.
(5)
Здесь
∂
∂n
— производнаяпо направлению внешней нормали. Первые
два равенства представляют собой начальные условия (
n
1
,
0
— началь-
наяконцентрациямолекул UF
6
)
. Третье равенство представляет собой
краевые условиятретьего рода [5, 6]. Если
r
k
= 0
, то это условие
отражает тот факт, что на границе области частицы вещества частич-
но поглощаютсяи частично отражаются. Если
r
k
= 0
, то это условие
описывает поступление вещества внутрь области через ее границу. Ко-
эффициенты
α
k
и
β
k
удовлетворяют условиям
|
α
k
|
+
|
β
k
|
= 0
,
α
k
β
k
≥
0
(эти условия связаны с теоремой о единственности решения);
r
k
— не-
котораяфункция, вид которой зависит от конкретной задачи.
Задачу (4), (5) можно разбить на две независимые задачи: дляуран-
содержащих и фторсодержащих продуктов. Это облегчает процесс ре-
шения.
Дляурансодержащих продуктов получаем следующую задачу:
∂
∂t
n
1
=
D
1
∆
n
1
−
(
v
1
,
grad
(
n
1
))
−
(
λ
1
+
K
)
n
1
+
F
1
(
x, t
)
,
∂
∂t
n
2
=
D
2
∆
n
2
−
(
v
2
,
grad
(
n
2
)) +
λ
1
n
1
−
(
λ
2
+
K
)
n
2
,
∂
∂t
n
3
=
D
3
∆
n
3
−
(
v
3
,
grad
(
n
3
)) +
λ
2
n
2
−
(
λ
3
+
K
)
n
3
,
∂
∂t
n
4
=
D
4
∆
n
4
−
(
v
4
,
grad
(
n
4
)) +
λ
3
n
3
−
Kn
4
, x
∈
Q, t
∈
(
t
0
, t
1
);
n
1
(
x, t
0
) =
n
1
,
0
(
x
)
, x
∈
Q,
n
k
(
x, t
0
) = 0
, k
= 2
,
4
, x
∈
Q,
α
k
(
x, t
)
∂
∂n
n
k
(
x, t
) +
β
k
(
x, t
)
n
k
(
x, t
) =
r
k
(
x, t
)
,
k
= 1
,
4
, x
∈
∂Q, t
∈
(
t
0
, t
1
)
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2005. № 4
99