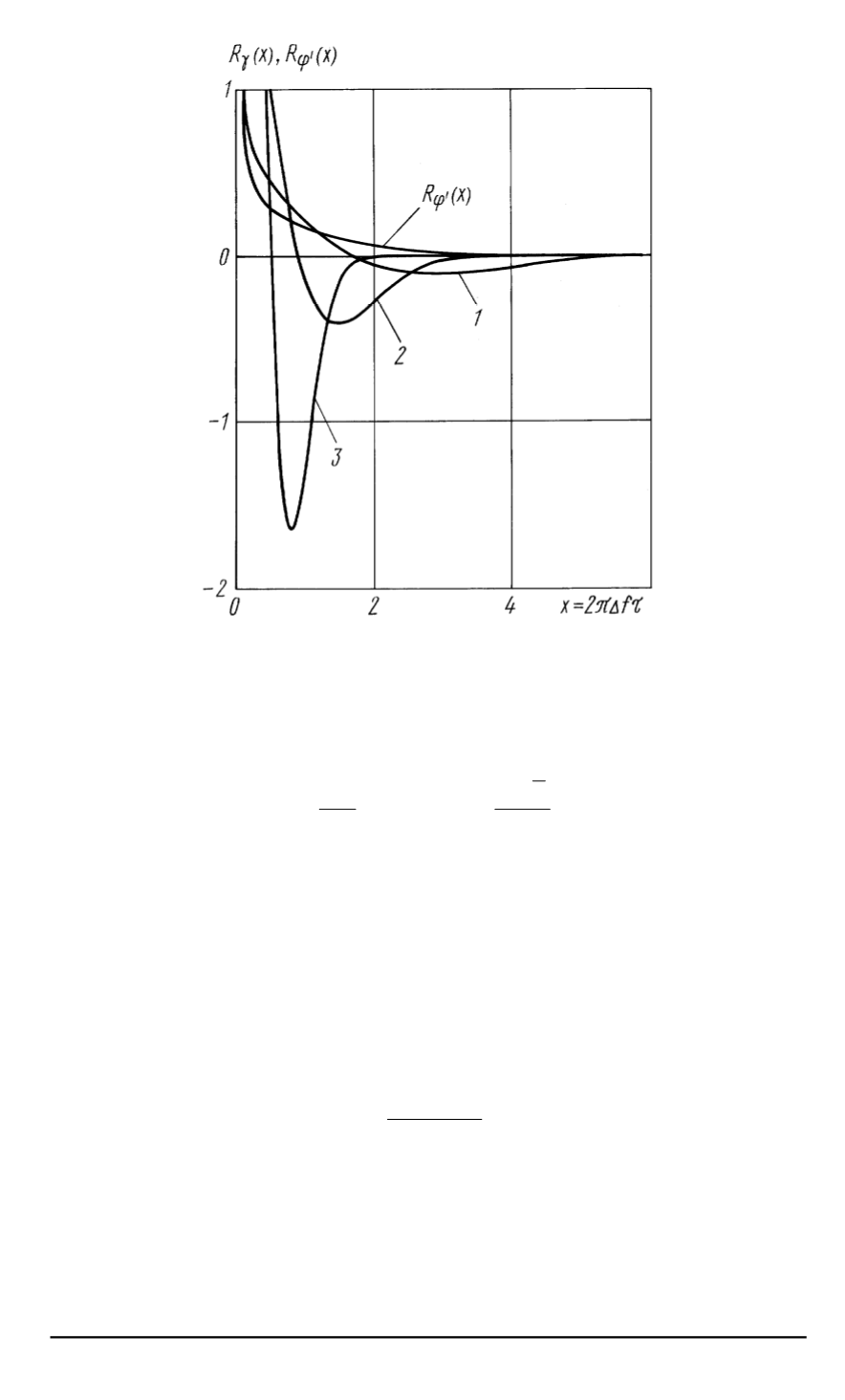
Рис
. 1.
Корреляционные функции логарифмической производной огибающей
квазигармонического шума
Итак
,
корреляционная функция
γ
(
t
)
имеет вид
R
γ
(
τ
) =
−
d
2
dτ
2
µ
(1 +
ρ
)
E
µ
2
√
ρ
1 +
ρ
¶¶
K
(
ρ
)
.
(5)
На рис
. 1
приведены рассчитанные по формуле
(5)
графики
R
γ
(
τ
)
(
1
–
3
)
для квазигармонического шума
ξ
(
t
)
с гауссовой формой спек
-
тральной плотности
,
когда
ρ
(
τ
) = exp(
−
π
(∆
f τ
)
2
)
,
где
∆
f
—
ширина
спектра шума
.
Для графиков
2
и
3
ширина спектра шума соответствен
-
но в
2
и
4
раза больше
,
чем для графика
1
.
Для сравнения на рис
. 1
показан график
R
ϕ
0
(
τ
)
—
корреляционной функции производной слу
-
чайной фазы процесса
ξ
(
t
)
,
вычисленной по известной формуле
[1]
R
ϕ
0
(
τ
) =
−
ρ
0
2
−
ρρ
00
2
ρ
2
ln(1
−
ρ
2
)
(6)
для ширины спектра такой же
,
как для графика
1
.
Из рис
. 1
видно
,
что для корреляционных функций случайного про
-
цесса
γ
(
t
)
,
определяемых формулой
(5),
характерно наличие участков
положительной и отрицательной корреляции
,
тогда как корреляцион
-
ные функции
,
рассчитанные по формуле
(6),
содержат только участок
6
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2


