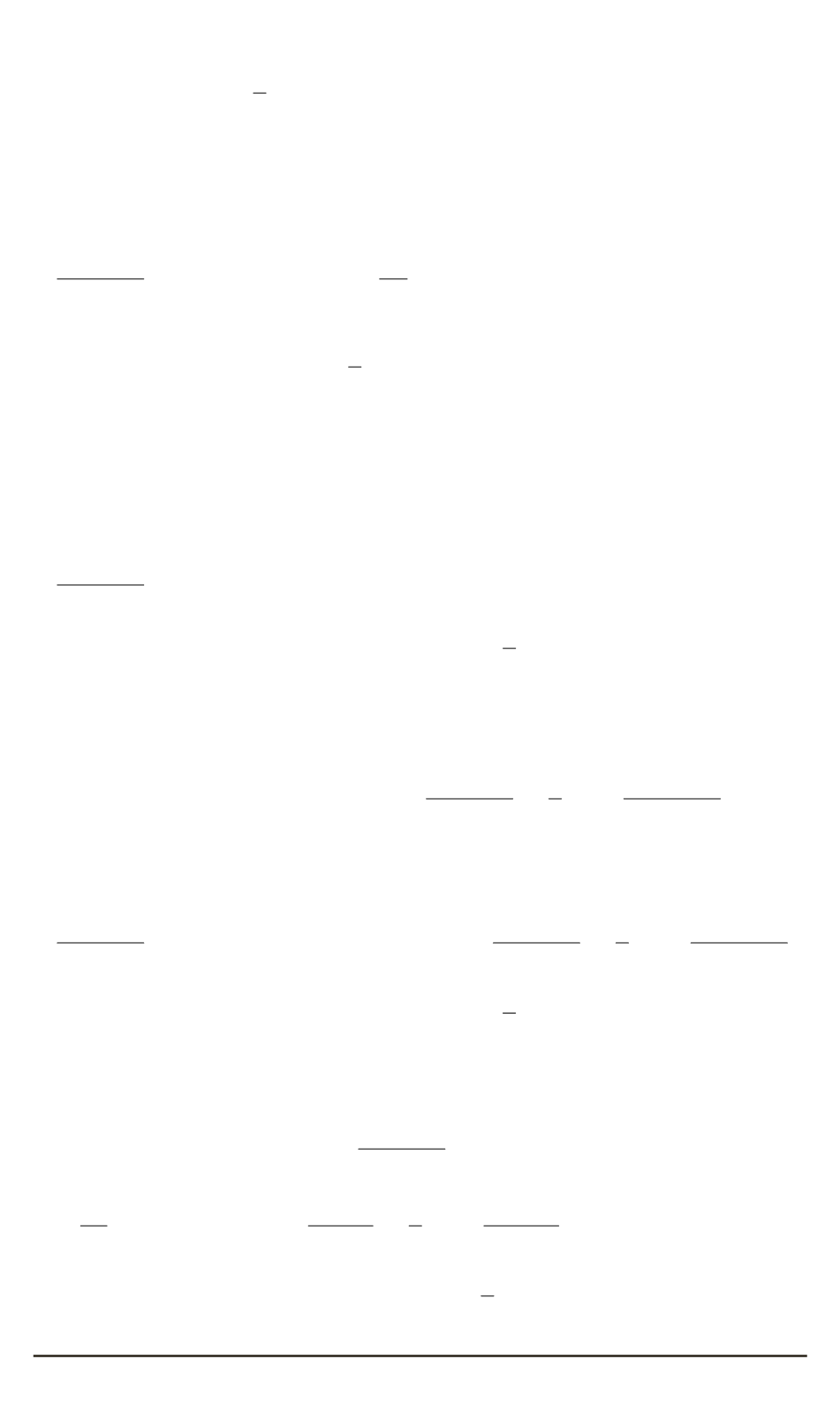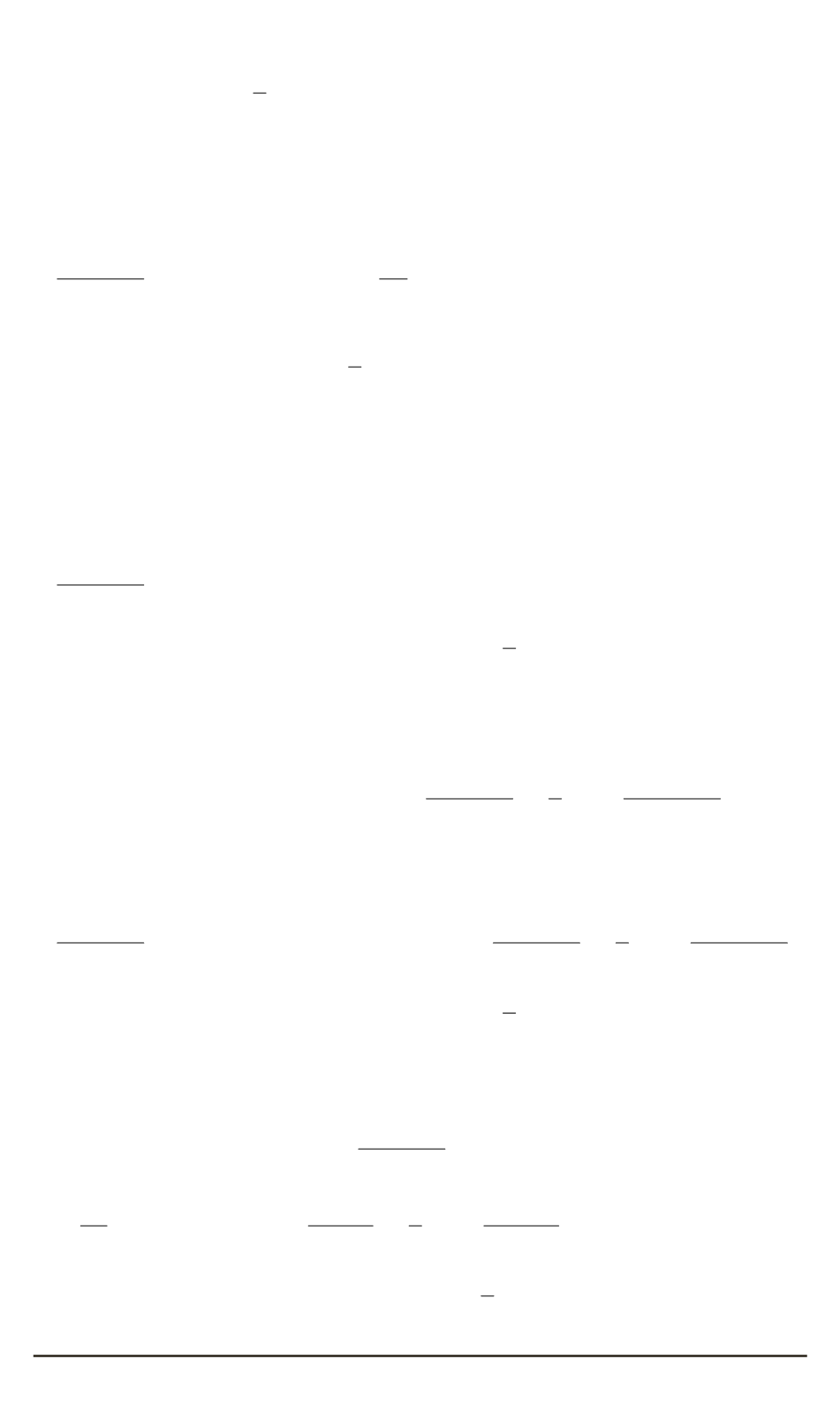
Формула (18) является первым приближением при разложении в ряд
экспоненты
exp
−
1
2
D
ξ
μ
2
ξ
в выражении (17).
В общем случае уравнение для характеристической функции
g
(
λ
;
t
)
, описывающей флуктуации скорости броуновской частицы
(см. (15)), имеет вид
∂g
(
λ
;
t
)
∂t
=
iλF
m
(
t
)
g
(
λ
;
t
) +
ν
τ
2
π
∞
Z
−∞
∞
Z
−∞
(exp (
−
iD
γ
λV
)
−
1) +
+ exp
−
1
2
D
ξ
λ
2
−
1 e
i
(
λ
−
μ
)
V
g
(
μ
;
t
)
dμdV.
(19)
При выводе формулы (19) учтены выражения (16) и (17) для характе-
ристических функций процессов
W
γ
(
t
)
и
W
ξ
(
t
)
.
Нахождение интегралов в формуле (19) позволяет получить урав-
нение для характеристической функции
g
(
λ
;
t
)
:
∂g
(
λ
;
t
)
∂t
=
iλF
m
(
t
)
g
(
λ
;
t
) +
ν
τ
(
g
((1
−
D
γ
)
λ
;
t
)
−
g
(
λ
;
t
)) +
+
ν
τ
exp
−
1
2
D
ξ
λ
2
−
1
g
(
λ
;
t
)
.
(20)
Разложив в ряд функцию
g
((1
−
D
γ
)
λ
;
t
)
при
D
γ
1
и сохранив
только первые три члена, запишем
g
((1
−
D
γ
)
λ
;
t
) =
g
(
λ
;
t
)
−
D
γ
λ
∂g
(
λ
;
t
)
∂λ
+
1
2
D
2
γ
λ
2
∂
2
g
(
λ
;
t
)
∂λ
2
.
(21)
С учетом формулы (21) в этом приближении уравнение (20) принимает
вид
∂g
(
λ
;
t
)
∂t
=
iλF
m
(
t
)
g
(
λ
;
t
) +
ν
τ
−
D
γ
λ
∂g
(
λ
;
t
)
∂λ
+
1
2
D
2
γ
λ
2
∂
2
g
(
λ
;
t
)
∂λ
2
+
+
ν
τ
exp
−
1
2
D
ξ
λ
2
−
1
g
(
λ
;
t
)
.
(22)
Далее будем полагать детерминированную силу постоянной:
F
m
(
t
) =
F
0
/m
=
const. Тогда можно записать уравнение (22) для
стационарного случая, когда
∂g
(
λ
;
t
)
∂t
= 0
:
iλ
F
0
m
g
(
λ
) +
ν
τ
−
D
γ
λ
dg
(
λ
)
dλ
+
1
2
D
2
γ
λ
2
d
2
g
(
λ
)
dλ
2
+
+
ν
τ
exp
−
1
2
D
ξ
λ
2
−
1
g
(
λ
) = 0
.
(23)
32
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 3