Введение.
Существуют различные подходы к построению матема-
тической модели теплопереноса в композите с шаровыми включения-
ми, на основе которой можно получить оценки эффективного коэффи-
циента теплопроводности такого композита [1–8]. Однако большин-
ство подходов учитывает лишь объемную концентрацию включений и
не принимает во внимание их взаимное расположение. Обычно пред-
полагают, что шаровые включения распределены по объему компо-
зита равномерно, но их взаимное расположение является случайным
(хаотическим). Сравнительный анализ подходов проведен в работах
[9, 10].
В работах [11, 12] приведена методика построения двусторонних
оценок эффективного коэффициента теплопроводности, основанная
на рассмотрении процесса теплопереноса в представительном эле-
менте изотропного композита матричной структуры. В случае шаро-
вых включений обычно выделяют представительный элемент в виде
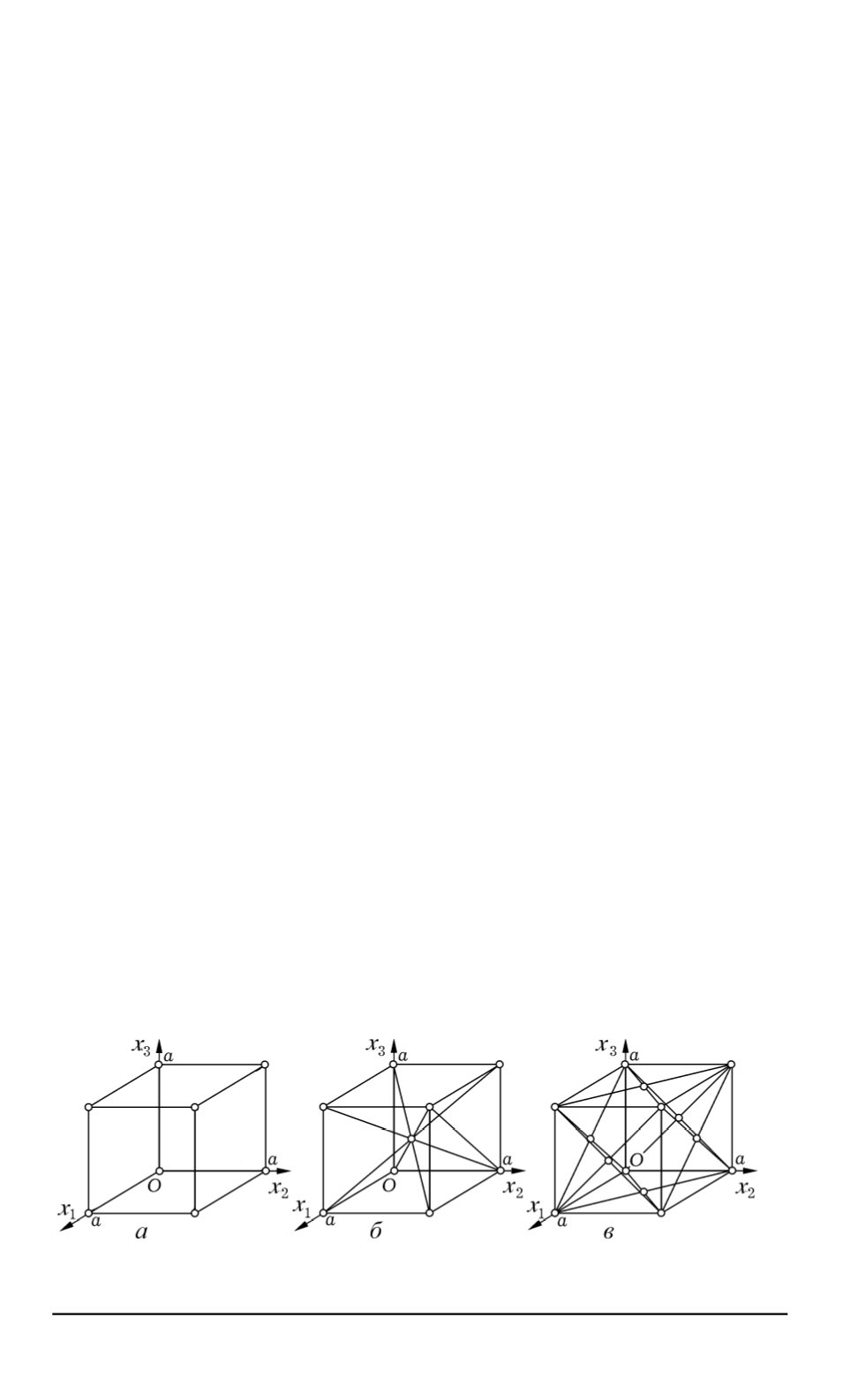
куба, в центр которого помещают включение [12]. Такая конфигу-
рация представительного элемента эквивалентна простой кубической
(ПК) кристаллической решетке, повторяющаяся ячейка которой пока-
зана на рис. 1,
а
. Для однонаправленного трансверсально изотропного
волокнистого композита представительным элементом его структуры
служит квадрат с расположенным в нем поперечным сечением волокна
[12–14].
Для получения верхней оценки эффективного коэффициента те-
плопроводности принимают предположение о равномерном распо-
ложении в представительном элементе изотермических плоскостей
параллельно одной из граней куба (в плоском представительном
элементе предполагают, что изотермы параллельны одной из сто-
рон квадрата). Указанное распределение температуры допустимо для
минимизируемого функционала, входящего в вариационную форму-
лировку задачи стационарной теплопроводности [15, 16] в рассма-
триваемом представительном элементе структуры композита, но не
совпадает с истинным распределением, на котором этот функционал
достигает минимума. Поэтому вычисленная по такому распределению
Рис. 1. Повторяющиеся ячейки простой кубической (
а
), объемноцентрирован-
ной (
б
) и гранецентрированной (
в
) кристаллических решеток
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
95


