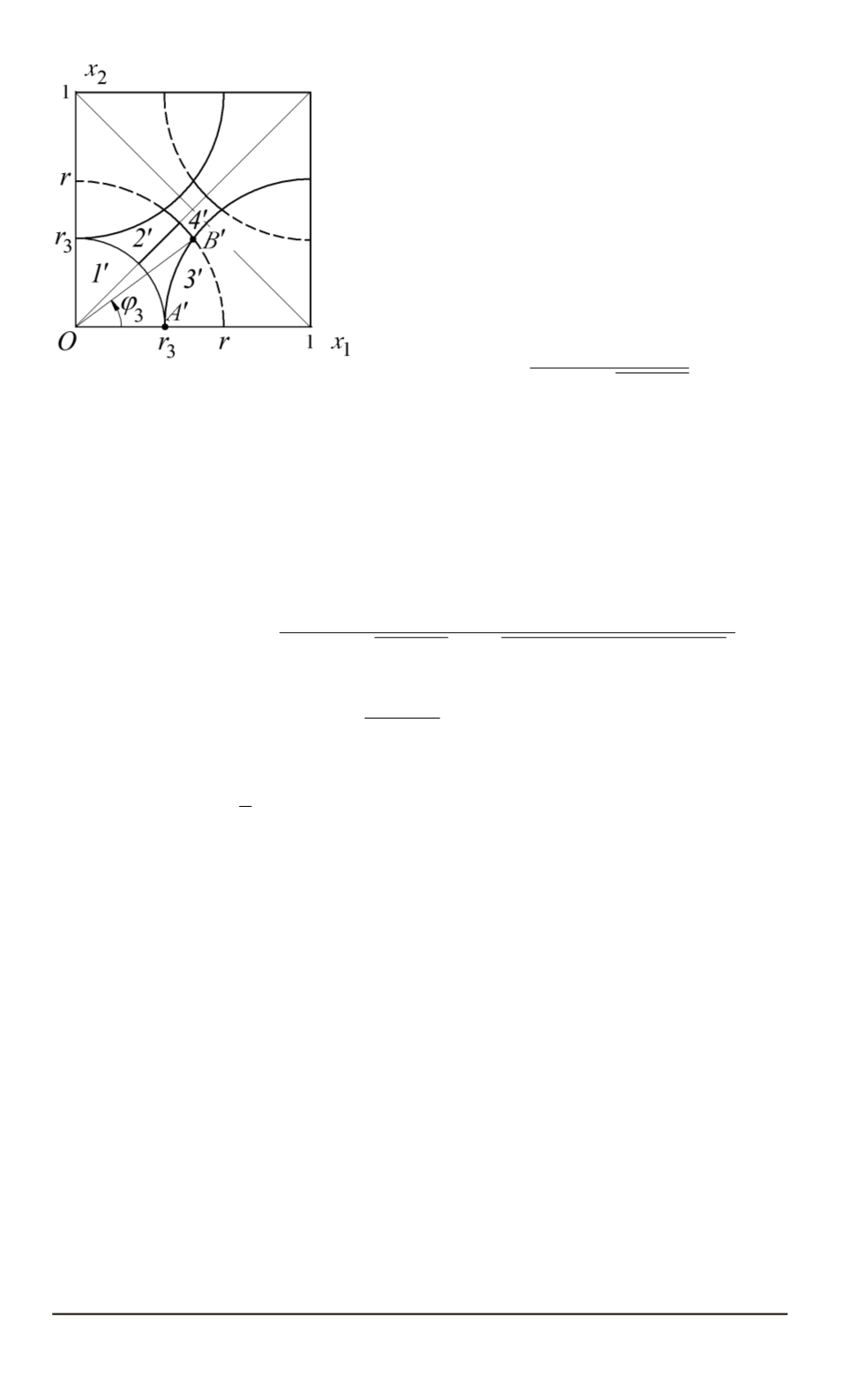
Рис. 3. Разбиение ячейки ГЦК-
решетки на подобласти (
1
0
–4
0
)
косинусов запишем
r
2
= 1 +
+
ρ
2
−
2
ρ
cos(
π/
4
−
ϕ
)
. Откуда следует
уравнение дуги
A
0
B
0
ϕ
0
(
r, ρ
) =
π/
4
−
arccos((1+
ρ
2
−
r
2
)
/
(2
ρ
))
.
Тогда составляющую проводимости
рассматриваемого элемента, соответ-
ствующую подобласти
2
0
, можно пред-
ставить интегралом
Y
0
2
= 2
r
Z
r
3
π/
4
−
ϕ
0
(
r, ρ
)
1 +
b
1
p
r
2
−
ρ
2
ρdρ.
Подобласть
3
0
ограничена дугой ра-
диусом
r
окружности c центром в начале полярной системы координат
(см. рис. 3), координатной осью
Ox
1
и дугой
A
0
B
0
, при этом
ϕ
2
[0;
ϕ
3
]
,
где
ϕ
3
= arccos(1
/
(2
r
))
. Для этой подобласти составляющая проводи-
мости указанного представительного элемента равна
Y
0
3
=
r
Z
r
3
ρdρ
ϕ
0
(
r,ρ
)
Z
0
dϕ
1 +
b
1
(
p
r
2
−
ρ
2
+
p
r
2
−
ρ
2
−
1 + 2
ρ
cos
ϕ
)
.
Наконец, для составляющей проводимости, соответствующей под-
области
4
0
, имеем
Y
0
4
= 1
− √
4
r
2
−
1
−
(
π
−
4
ϕ
3
)
r
2
.
Квадрат, представленный на рис. 3, включает в себя по четыре под-
области
1
0
,
2
0
и
3
0
и подобласть
4
0
. В итоге для искомой нижней оценки
при
r
2
(1
/
2; 1
/
√
2)
, равной суммарной относительной тепловой про-
водимости представительного элемента, находим
e
λ
−
2
= 4(
Y
0
1
+
Y
0
2
+
Y
0
3
) +
Y
0
4
.
Результаты расчетов.
Сравнительный количественный анализ по-
лученных выше расчетных зависимостей для верхних (
e
λ
+
) и ниж-
них (
e
λ
−
) безразмерных оценок эффективного коэффициента теплопро-
водности композита матричной структуры показал следующее: при
ˉ
λ
= (
λ
◦
/λ
m
)
2
[0
,
5; 2]
взаимное расположение шаровых включений
относительно слабо влияет на эти оценки. Для трех рассмотренных
вариантов взаимного расположения включений такие оценки при из-
менении объемной концентрации
C
V
включений лежат внутри срав-
нительно узкой полосы, ограниченной двусторонними оценками
e
λ
+
0
= 1
−
C
V
+
C
V
ˉ
λ
;
e
λ
−
0
= 1
/
(1
−
C
V
+
C
V
/
ˉ
λ
)
,
(8)
которые следуют из смесевых моделей механики композитов [19] или
из вариационной формулировки задачи стационарной теплопровод-
102
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5


