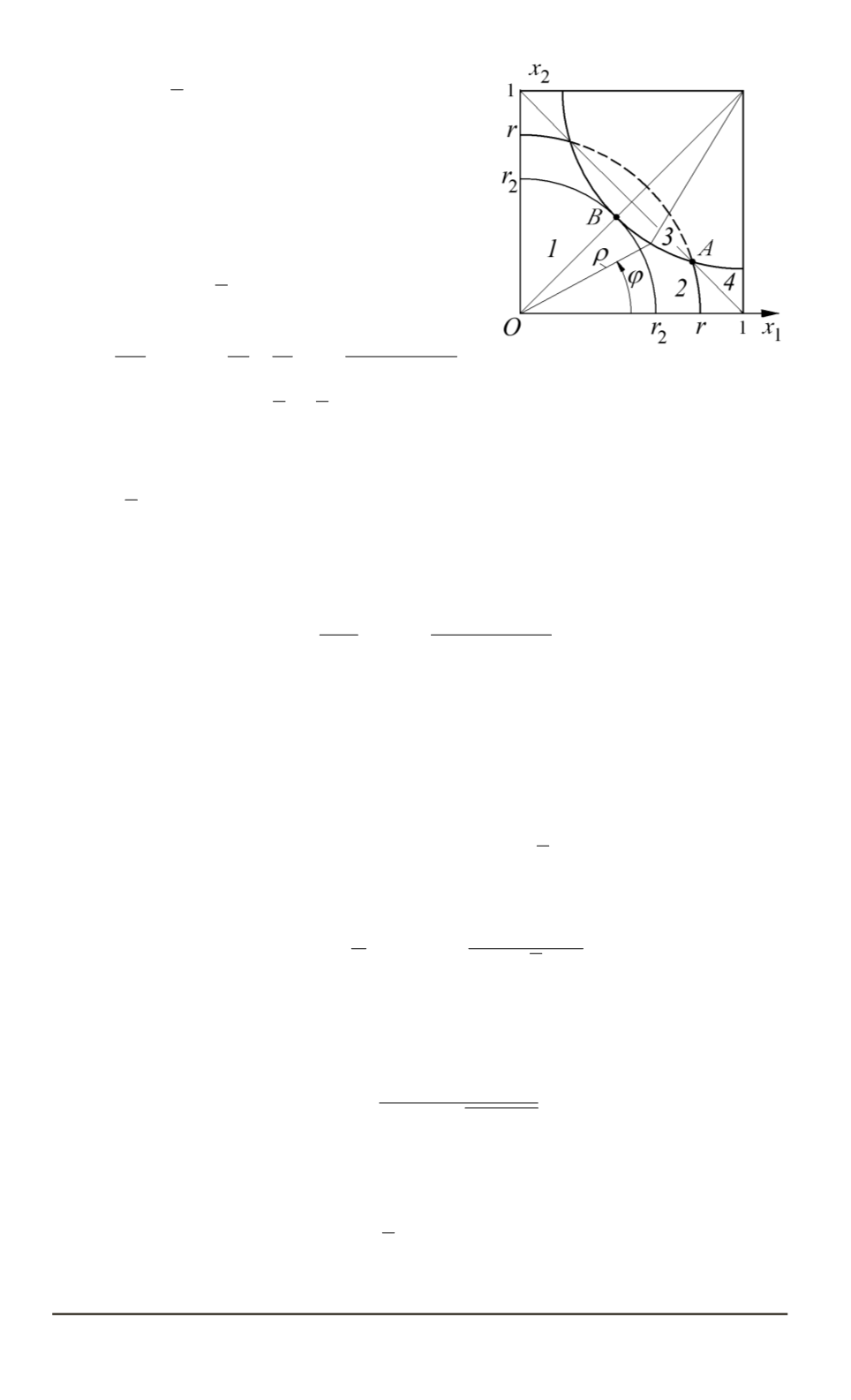
Рис. 2. Разбиение ячейки ОЦК-
решетки на подобласти (
1
–
4
)
В итоге для искомой оценки при
1
/
2
< r
6
√
3
/
2
запишем
b
λ
+
2
= 1
/
(2
R
0
2
+
R
00
2
)
.
При построении для рассматриваемо-
го представительного элемента нижней
оценки
λ
−
2
, модифицировав формулу (4)
при
r
2
(0; 1
/
√
2]
, получим
e
λ
−
2
=
λ
−
2
λ
m
= 1
−
π
r
2
2
+
π
b
1
r
−
ln(1 +
b
1
r
)
b
1
.
а в случае
r
2
(1
/
√
2;
√
3
/
2)
для вычи-
сления интеграла в формуле (2) выделим несколько подобластей ин-
тегрирования (рис. 2). Подобласть
1
— сектор окружности радиусом
r
2
=
√
2
−
r
и углом
π/
2
при вершине. Составляющая относительной
тепловой проводимости элемента, соответствующая этой подобласти,
после модификации формулы (4) может быть представлена в виде
Y
1
=
π/
2
b
1
r
2
−
ln(1 +
b
1
r
2
)
b
1
.
Подобласть
2
ограничена дугами окружностей радиусами
r
2
и
r
,
координатной осью
Ox
1
и дугой
AB
радиусом
r
окружности с центром
в точке с координатами
x
1
=
x
2
= 1
(см. рис. 2). Если перейти к
полярной системе координат с началом при
x
1
=
x
2
= 0
, радиальной
координатой
ρ
и отсчетом полярного угла
ϕ
от оси
Ox
1
, то согласно
теореме косинусов запишем
r
2
= 2 +
ρ
2
−
2
√
2
ρ
cos(
π/
4
−
ϕ
)
. Откуда
получим уравнение дуги
AB
:
ϕ
(
r, ρ
) =
π
4
−
arccos
2 +
ρ
2
−
r
2
2
√
2
ρ
.
Тогда составляющую проводимости рассматриваемого элемента, со-
ответствующую подобласти
2
, можно представить интегралом
Y
2
=
r
Z
r
2
ϕ
(
r, ρ
)
ρdρ
1 +
b
1
p
r
2
−
ρ
2
.
Подобласть
3
ограничена дугами радиусом
r
окружностей c цен-
трами в точках с координатами
x
1
=
x
2
= 0
и
x
1
=
x
2
= 1
(см. рис. 2),
при этом
ϕ
2
=
π/
4
−
arccos(
√
2
/
(2
r
))
≤
ϕ
≤
π/
4
. Для этой подобласти
составляющая проводимости рассматриваемого представительного
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 5
99


