Пусть
C
01
6
= 0
, тогда
C
11
=
C
21
=
C
31
=
C
41
=
. . .
=
C
N
1
=
=
C
01
(
−
β/γ
)
, где
β
и
γ
— комплексы, входящие в (12). Из системы (12)
также имеем:
C
03
=
C
01
cos (Λ
l
) ;
C
04
=
C
03
tg (Λ (
l
0
−
l
)) =
C
01
cos (Λ
l
)
×
×
tg (Λ (
l
0
−
l
))
, т.е. все константы выражены через
C
01
. Частотное
уравнение принимает вид
EF
0
˜
A
−
1
00
λ
1
/
2
tg ˜
A
−
1
00
λ
1
/
2
l
−
Nk
+
+
EF
0
˜
A
−
1
00
λ
1
/
2
tg ˜
A
−
1
00
λ
1
/
2
(
l
0
−
l
)
−
−
N
−
k
2
cos ˜
A
−
1
jj
λ
1
/
2
l
−
EF
˜
A
−
1
jj
λ
1
/
2
sin ˜
A
−
1
jj
λ
1
/
2
l
+
k
cos ˜
A
−
1
jj
λ
1
/
2
l
= 0
.
В качестве примера рассмотрим систему с четырьмя боковыми
стержнями. Кроме описанного выше способа для этого примера мож-
но записать частотное уравнение для всей системы, вычислив опреде-
литель матрицы
Δ
и приравняв его нулю. Приведем его вид
γ
4
(Λ sin (Λ (
l
0
−
l
)) cos (Λ
l
)
EF
0
Λ+
+ Λ cos (Λ (
l
0
−
l
)) (
EF
0
Λ sin (Λ
l
) + 4
β
))
−
−
4
αβγ
3
Λ cos (Λ (
l
0
−
l
)) = 0
.
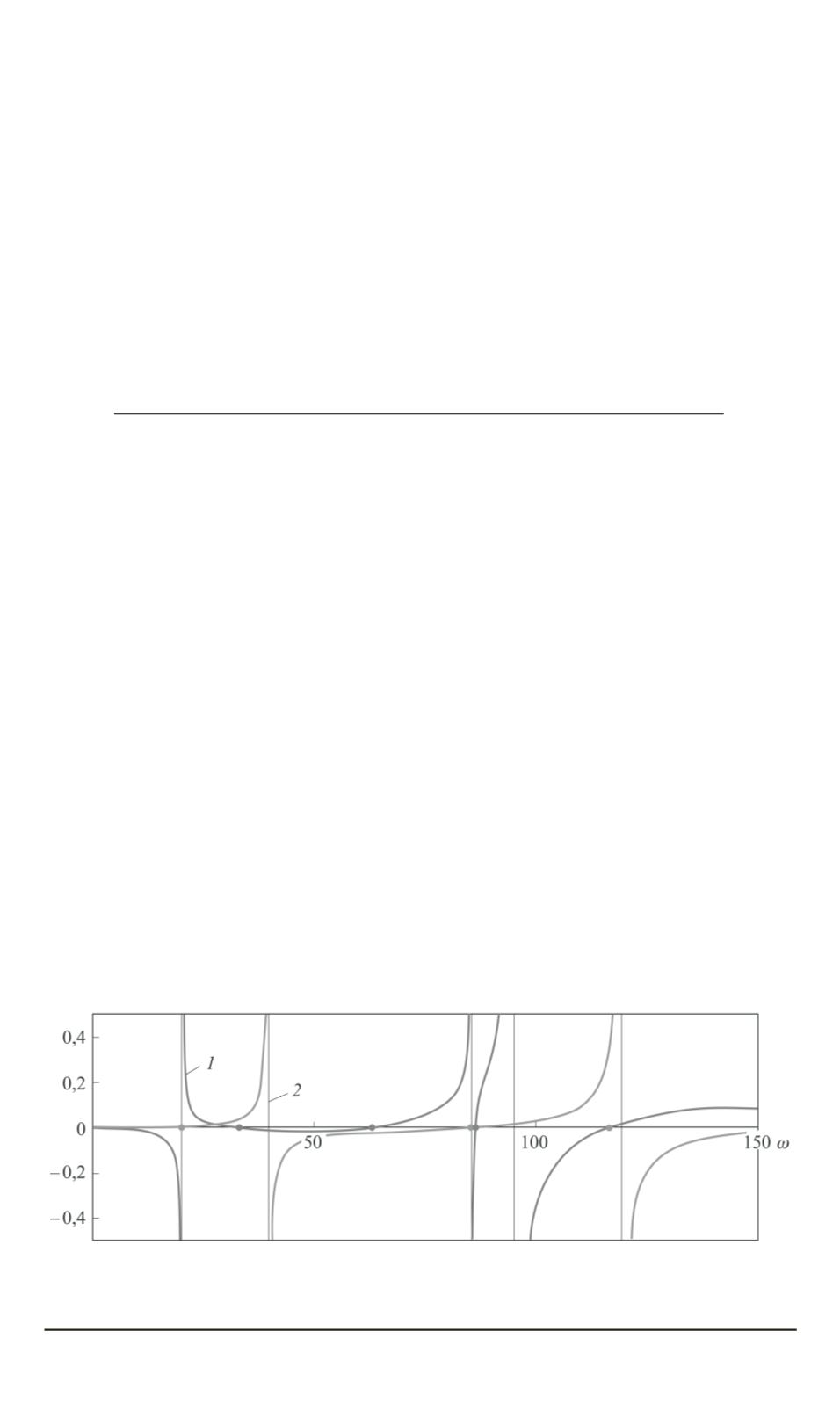
Графики трансцендентных частотных уравнений для рассмотрен-
ных выше случаев представлены на рис. 2. В качестве исходных дан-
ных были приняты следующие:
EF
= 2
∙
10
9
Н;
EF
0
= 2
,
2
∙
10
9
Н;
k
= 7
∙
10
7
Н/м;
m
= 5900
кг/м;
m
0
= 6000
кг/м;
l
= 23
;
l
0
= 33
м.
Значения первых трех частот колебаний рассматриваемой схемы при-
ведены ниже:
n
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
2
3
ω
, рад/с . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20,08 31,53 63,50
Рис. 2. Графики трансцендентных частотных уравнений для
C
01
6
= 0
6
6
(
1
) и
C
01
= 0
(
2
)
62
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6


