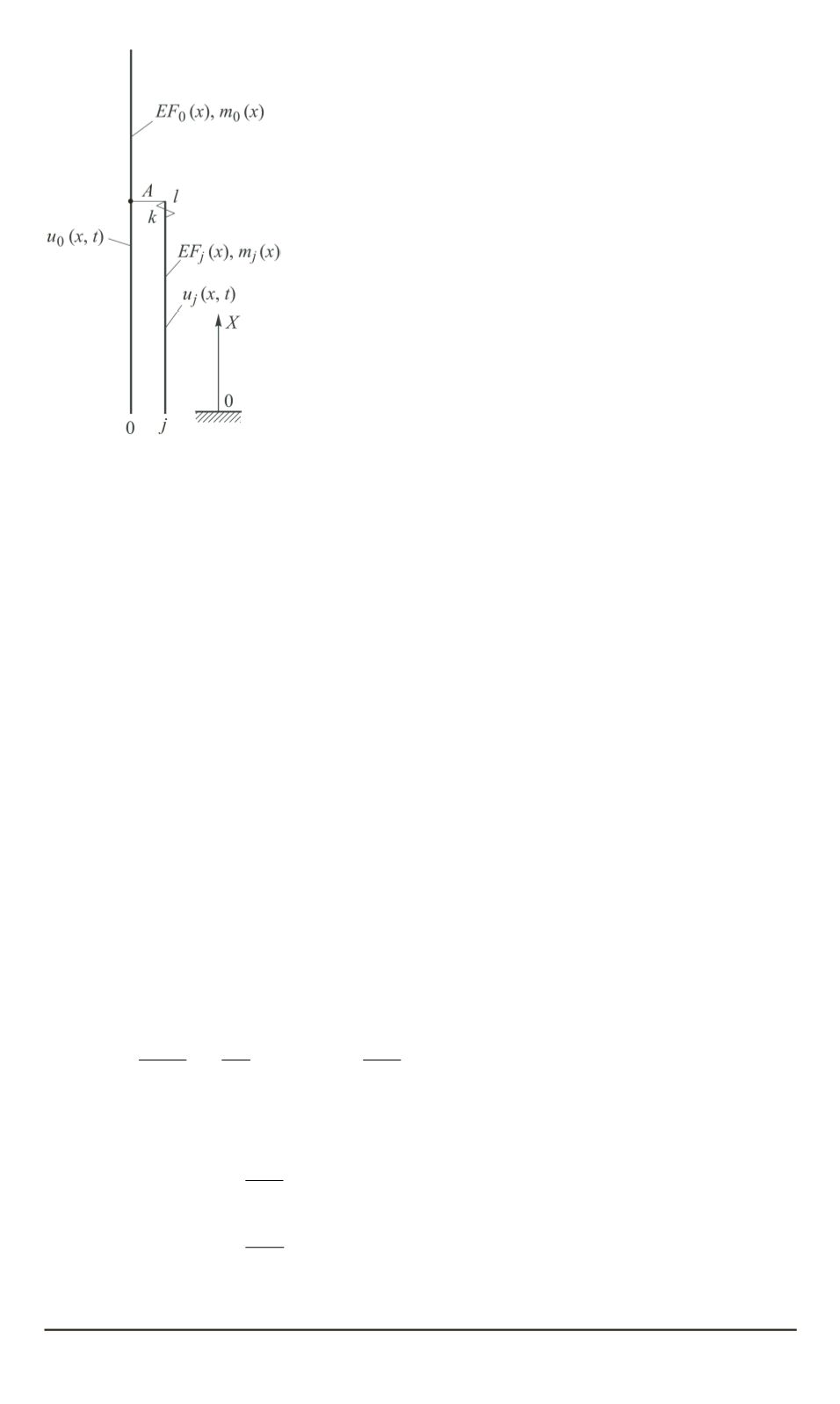
Рис. 1. Схема централь-
ного стержня
Исследования колебаний пакетных конструк-
ций наталкиваются на определенные трудно-
сти, связанные с динамическим воздействи-
ем боковых и центрального блоков [1–6]. В
случае симметрии компоновки РН сложное,
пространственное взаимодействие блоков па-
кетной конструкции можно разделить на ко-
нечное число типов колебаний, одним из ко-
торых являются продольные колебания цен-
трального и боковых блоков [7]. Математи-
ческая модель продольных колебаний подоб-
ной конструкции в виде пакета тонкостенных
стержней подробно рассмотрена в работе [8].
В настоящей статье приведены теоретиче-
ские и вычислительные результаты продоль-
ных колебаний пакета стержней, дополняющие исследование, выпол-
ненное А.А. Пожалостиным [8].
Постановка задачи.
Рассмотрим другие продольные колебания
пакета стержней, состоящего из центрального стержня длиной
l
0
и
N
боковых стержней одинаковой длины
l
j
=
l
,
(
l
0
> l
j
)
,
j
= 1
,
2
, . . . , N,
скрепленных в точке
А
(
x
A
=
l
)
(рис. 1) с центральными пружинными
элементами жесткостью
k
.
Введем неподвижную систему отсчета
ОХ
и предположим, что
жесткость стержней
EF
j
(
x
)
, распределенная масса
m
j
(
x
)
и возмуще-
ние
q
(
x, t
)
являются ограниченными функциями координаты
x
:
0
< r
j
≤
EF
j
(
x
)
≤
R
j
;
0
< m
j
≤
m
j
(
x
)
≤
M
j
;
0
< q
j
≤
q
j
(
x, t
)
≤
Q
j
, j
= 0
,
1
,
2
, . . . , N.
(1)
Пусть при продольных колебаниях в сечениях стержней с коорди-
натой
x
возникают смещения
u
j
(
x, t
)
, определяемые по уравнениям
m
j
(
x
)
∂
2
u
j
∂t
2
−
∂
∂x
EF
j
(
x
)
∂u
j
∂x
=
q
j
(
x, t
)
, j
= 0
,
1
,
2
, . . . , N,
(2)
граничными условиями отсутствия нормальных сил на концах стерж-
ней
∂u
j
∂x
= 0
, x
= 0
, j
= 1
,
2
, . . . , N
;
∂u
0
∂x
= 0
, x
= 0
, x
=
l
0
;
(3)
условиями равенства нормальных сил, возникающих в стержнях,
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6


