(рис. 3,
а
), при второй — центральный стержень совершает колебания,
а боковые колеблются по одинаковой форме в фазе (рис. 3,
б
). Следу-
ет отметить, что первая и вторая частоты колебаний рассматриваемой
стержневой системы соответствуют колебаниям системы, состоящей
из твердых тел.
При колебании системы с третьей собственной частотой пер-
вый раз появляются узлы (рис. 3,
в
). Третья и последующие частоты
(рис. 3,
г
) соответствуют уже упругим колебаниям системы. С возра-
станием частоты колебаний, связанной с уменьшением влияния упру-
гих элементов, частоты и формы колебаний стремятся к парциальным
(рис. 3,
д
,
е
).
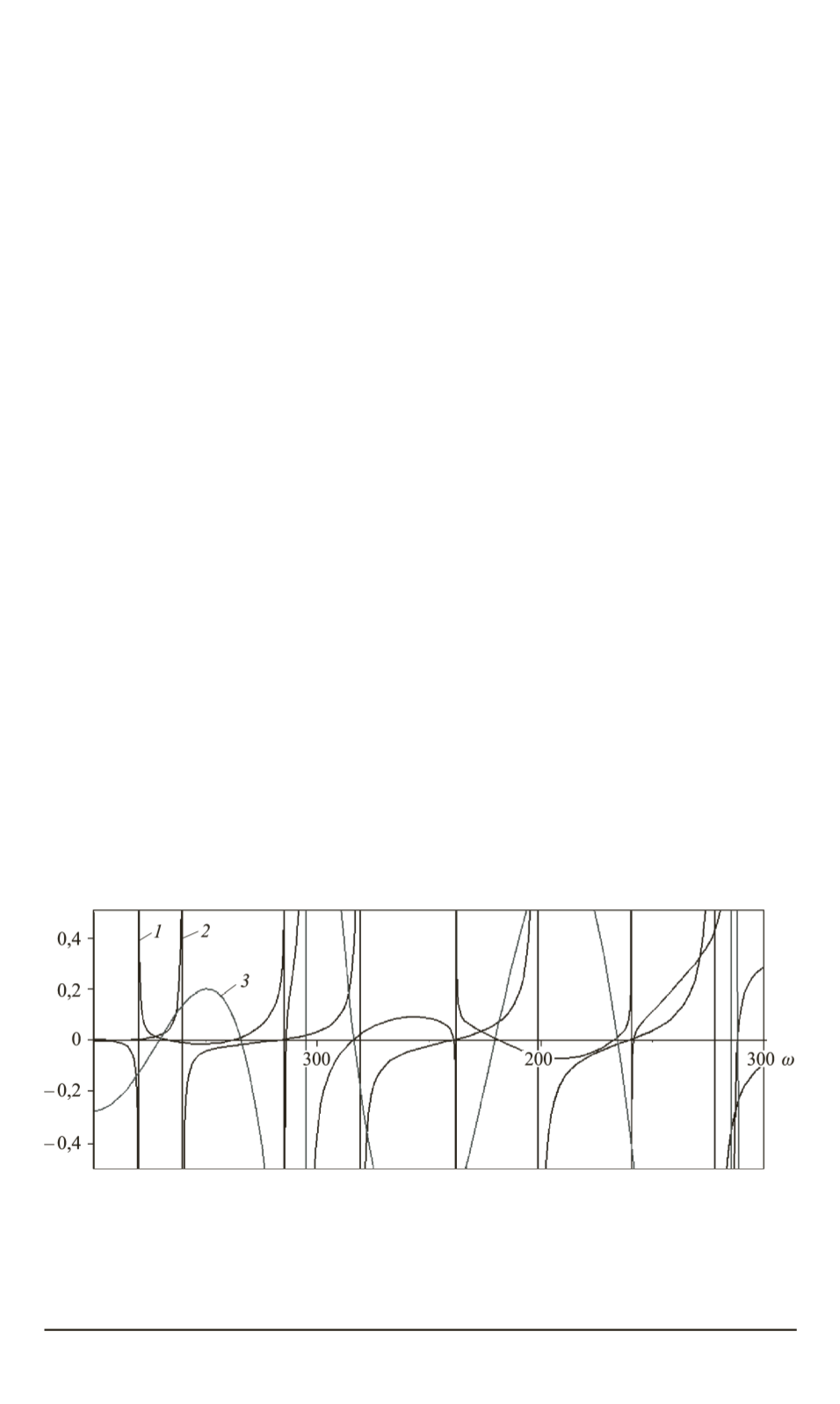
Кривые функций, точки пересечения которых с осью абсцисс явля-
ются решениями трансцендентных уравнений, представлены на рис. 4.
Согласно рисунку, собственные частоты колебаний системы распо-
ложены вблизи парциальных частот. Как было отмечено выше, при
увеличении частоты сближение собственных частот с парциальными
усиливается. В результате частоты, при которых колеблется вся си-
стема, условно разделяются на две группы: близкие к парциальным
частотам бокового стержня и частоты, близкие к парциальным часто-
там центрального стержня.
Выводы.
Рассмотрена задача о продольных колебаниях пакета
стержней. Описаны свойства поставленной краевой задачи и спектра
ее собственных значений. Предложено решение спектральной задачи
для произвольного числа однородных боковых стержней. Для числен-
ного примера найдены значения первых частот колебаний и постро-
ены соответствующие им формы. Также были выявлены некоторые
характерные свойства построенных форм колебаний.
Рис. 4. Кривые функций, точки пересечения которых с осью абсцисс являются
решениями трансцендентных уравнений, для
C
01
6
= 0
6
6
(
1
),
C
01
= 0
(
2
) совпадают
с первой парциальной системой (боковой стержень, закрепленный на упругом
элементе в точке
x
=
l
) и второй парциальной системы (
3
) (центральный
стержень, закрепленный на четырех упругих элементах в точке
A
)
64
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 6


