
— аварий на взрывоопасных объектах [1, 2];
— аварий на химически опасных объектах [3];
— разрушительных землетрясений [4];
— разрушения гидротехнических сооружений [5].
Рассматриваемая модель воздействия также используется для еди-
ничной реализации события при проведении заблаговременных рас-
четов по ожидаемым последствиям и оценке рисков.
Модель воздействия 2-го типа
задана функцией распределения
плотности вероятности случайной величины
Φ
f
(
x, y,
Φ)
(рис. 1,
а
).
В качестве случайных величин
Φ
рассматриваются параметры пора-
жающих факторов, вызывающих основные разрушения и поражения
(см. табл. 1).
Модель воздействия 3-го типа
определена функцией распределе-
ния
F
(
x, y,
Φ)
случайной величины
Φ
, характерной для рассматривае-
мой ЧС (рис. 1,
б
).
Основное свойство функции распределения плотности вероятно-
сти
f
(
x, y,
Φ)
— равенство единице площади, заключенной между кри-
вой, описываемой этой функцией и осью
Φ
(см. рис. 1,
а
) [8].
Функция распределения
F
(
x, y,
Φ)
случайной величины интенсив-
ности воздействия поражающего фактора, характерной для рассматри-
ваемой ЧС, — вероятность того, что случайная величина
Φ
в точке с
координатами
x, y
примет значение не выше заданного значения
Φ
з
:
F
(
x, y,
Φ) =
Р
(Φ
≤
Φ
з
)
.
При построении функции распределения
F
(
x, y,
Φ)
необходи-
мо учитывать ее свойства:
F
(
x, y,
Φ)
— функция неубывающая;
F
(
−∞
) = 0
;
F
(+
∞
) = 1
.
Функции
f
(
x, y,
Φ)
и
F
(
x, y,
Φ)
природных опасностей получают-
ся на основе статистической обработки результатов наблюдений за
опасными событиями. Для примера рассмотрим функции распределе-
ния интенсивности землетрясений
f
(
I
)
и
F
(
I
)
для Алтае-Саянского и
Прибайкальского регионов (рис. 2).
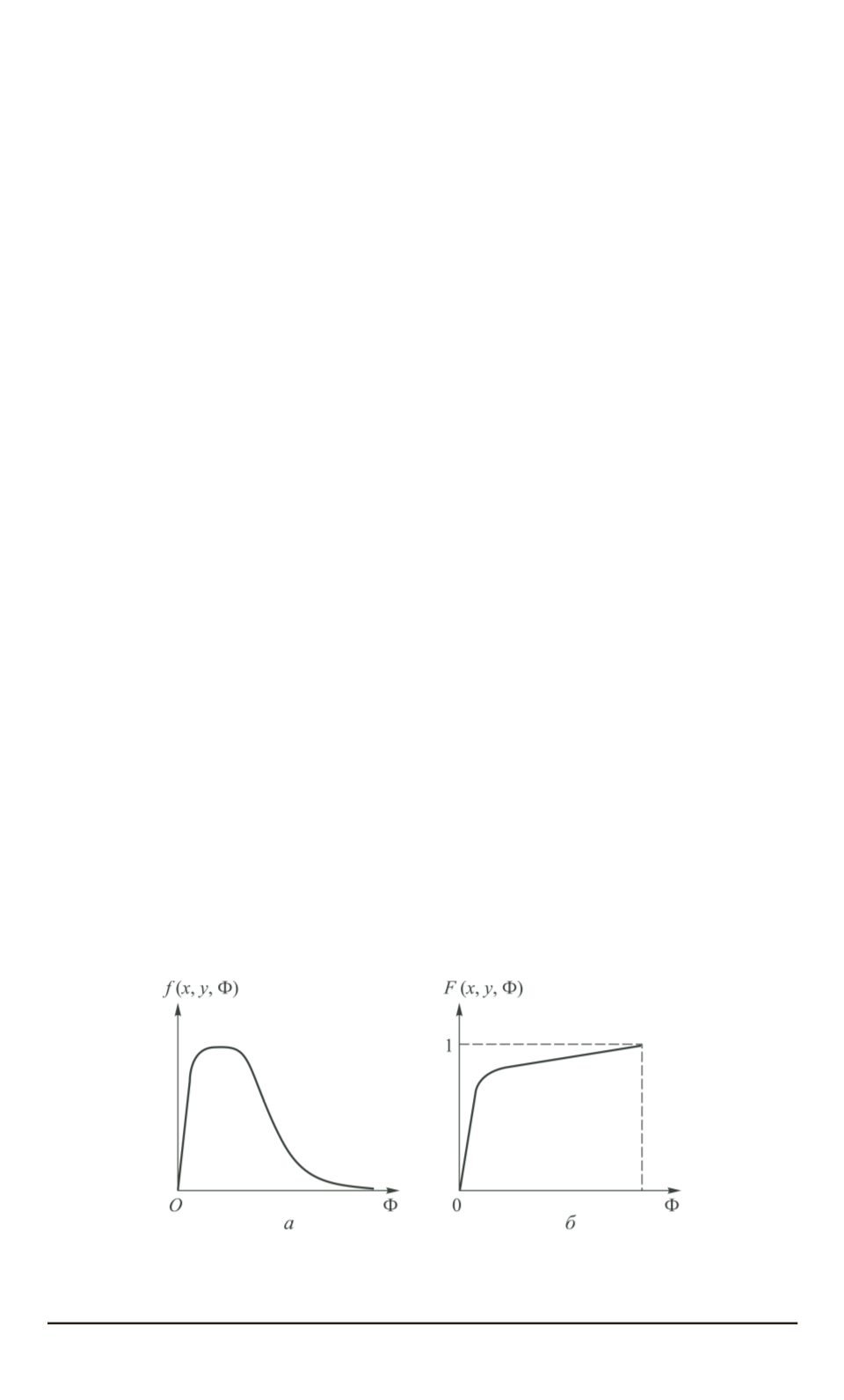
Рис. 1. Законы распределения поражающих факторов
Φ
в точке с координатами
x
,
y
:
а
— функции распределения плотности вероятностей;
б
— функции распределения
116
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 1

















