
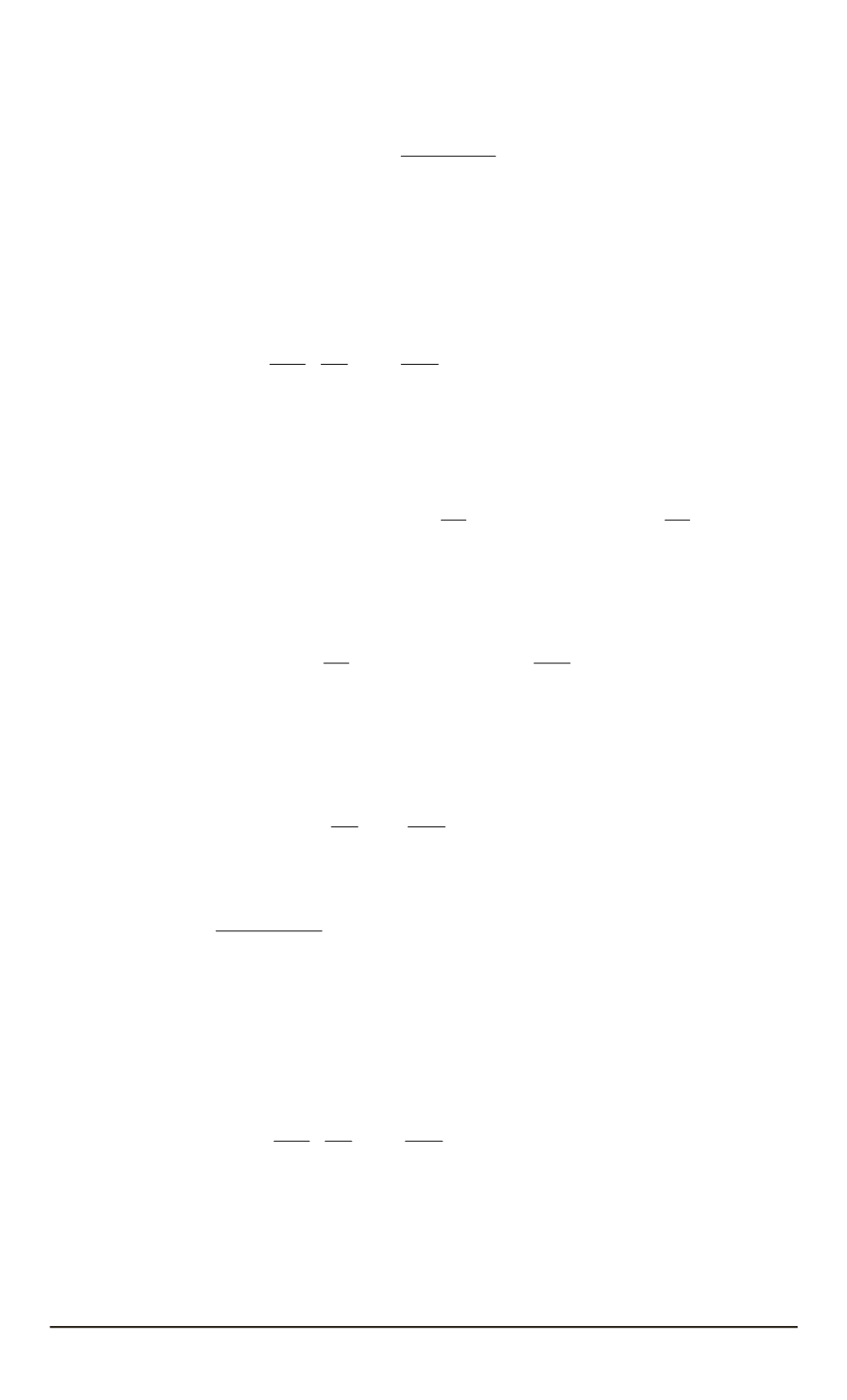
Здесь
g
(
γ
0
,β
)
(
z
0
, z
)
— функция, аналитическая по переменным
z
0
, z
, так
как
|
g
(
γ
0
,β
)
(
z
0
, z
)
|
6
∞
X
α
0
,α
=0
|
z
0
|
α
0
|
z
|
α
α
0
!
α
!
|
q
(
α
0
,α
)
(
γ
0
,β
)
|
6
e
|
z
0
|
+
|
z
|
.
Аналогично теореме 3.1, приведенной в работе [13], можно доказать,
что
g
(
γ
0
,β
)
(
z
0
, z
) = lim
t
→∞
G
(
γ
0
,β
)
(
t
;
z
0
, z
)
,
и функция
g
(
γ
0
,β
)
(
z
0
, z
)
удовле-
творяет стационарному первому уравнению
h
∂
∂z
0
,
∂
∂z
−
∂
k
∂z
k
g
(
γ
0
,β
)
(
z
0
, z
) = 0
.
(19)
Введем также двойные производящие функции для вероятностей
остановки,
|
u
|
6
1
,
g
β
(
z, u
) =
∞
X
n
=0
g
(
n,β
)
(0
, z
)
u
n
=
∞
X
α
=0
z
α
α
!
∞
X
n
=0
q
(0
,α
)
(
n,β
)
u
n
=
∞
X
α
=0
z
α
α
!
ϕ
αβ
(
u
)
(20)
и дифференциальный оператор
h u,
d
dz
=
∞
X
γ
0
,γ
=0
p
γ
0
γ
u
γ
0
d
γ
dz
γ
.
Лемма 5.
Экспоненциальная производящая функция
g
β
(
z, u
)
удов-
летворяет обыкновенному дифференциальному уравнению
h u,
∂
∂z
−
∂
k
∂z
k
g
β
(
z, u
) = 0
(21)
с граничными условиями
∂
α
g
β
(
z, u
)
∂z
α
|
z
=0
=
δ
α
β
, α
= 0
, . . . , k
−
1
.
(22)
J
Из уравнения (19) следует, что производящая функция,
|
u
|
6
1
,
e
g
β
(
z
0
, z
;
u
) =
∞
X
γ
0
=0
g
(
γ
0
,β
)
(
z
0
, z
)
u
γ
0
также удовлетворяет стационарному
первому уравнению
h
∂
∂z
0
,
∂
∂z
−
∂
k
∂z
k
e
g
β
(
z
0
, z
;
u
) = 0
.
(23)
Из описания марковского процесса
(
ξ
0
t
, ξ
t
)
следует соотношение
q
(
α
0
,α
)
(
γ
0
,β
)
=
(
0
,
γ
0
< α
0
;
q
(0
,α
)
(
γ
0
−
α
0
,β
)
, γ
0
∼
α
0
,
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
47

















