
Случайное блуждание
(
S
0
n
, S
n
)
в полуплоскости и задача о веро-
ятностях остановки.
На множестве состояний
Z
×
N
=
{
(
α
0
, α
)
, α
0
=
=
. . . ,
−
1
,
0
,
1
, . . . , α
= 0
,
1
, . . .
}
рассмотрим однородное случайное
блуждание
(
S
0
n
, S
n
)
, n
= 0
,
1
, . . .
Переходные вероятности за
n
ша-
гов обозначим
P
(
α
0
,α
)
(
β
0
,β
)
(
n
) = P
{
(
S
0
n
, S
n
) = (
β
0
, β
)
|
(
S
0
0
, S
0
) = (
α
0
, α
)
}
.
Пусть переходные вероятности за один шаг равны (
k
= 1
,
2
, . . .
)
P
{
(
S
0
n
+1
, S
n
+1
) = (
β
0
, β
)
|
(
S
0
n
, S
n
) = (
α
0
, α
)
}
=
p
β
0
−
α
0
,β
−
α
+
k
,
если
β
0
>
α
0
и
α
>
kβ
−
α
+
k
>
0
;
P
{
(
S
0
n
+1
, S
n
+1
) = (
β
0
, β
)
|
(
S
0
n
, S
n
) = (
α
0
, α
)
}
= 0
,
если
β
0
< α
0
;
P
{
(
S
0
n
+1
, S
n
+1
) = (
α
0
, α
)
|
(
S
0
n
, S
n
) = (
α
0
, α
)
}
= 1
,
если
α < k
.
Здесь задано распределение вероятностей
{
p
γ
0
γ
>
0
,
(
γ
0
, γ
)
∈
N
2
;
∞
X
γ
0
,γ
=0
p
γ
0
γ
= 1
, p
0
k
= 0
}
.
Для случайного блуждания
(
S
0
n
, S
n
)
возможна остановка в одном из
состояний множества
{
(
γ
0
, β
)
, γ
0
∈
Z, β
= 0
, . . . , k
−
1
}
. Вероятности
остановки равны
q
(
α
0
,α
)
(
γ
0
,β
)
= lim
n
→∞
P
(
α
0
,α
)
(
γ
0
,β
)
(
n
)
, γ
0
∈
Z, β
= 0
, . . . , k
−
1
,
(1)
и при
β
=
k
−
1
есть вероятности достижения границы полуплоскости
{
(
γ
0
, k
−
1)
, γ
0
∈
Z
}
, а при
β
= 0
, . . . , k
−
2
— вероятности перескока
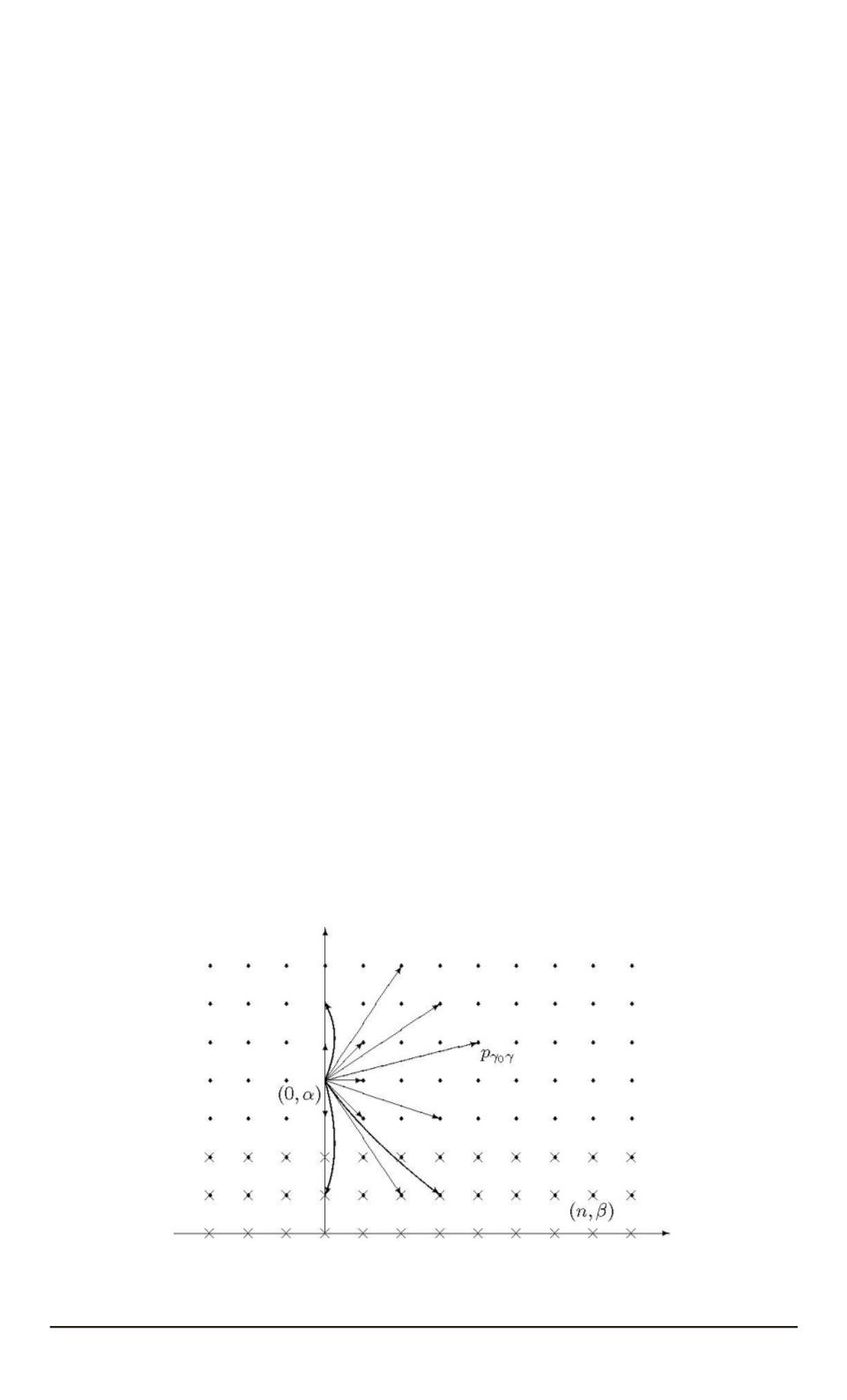
этой границы. Скачки случайного блуждания
(
S
0
n
, S
n
)
из состояния
(0
, α
)
и множество
{
(
γ
0
, β
)
, γ
0
∈
Z, β
= 0
, . . . , k
−
1
}
приведены на
рисунке.
Введем производящую функцию вероятностей скачков
h
(
u, s
) =
=
∞
X
γ
0
,γ
=0
p
γ
0
γ
u
γ
0
s
γ
,
|
u
|
6
1
,
|
s
|
6
1
. В работе получено выражение для ве-
Скачки случайного блуждания (
k
= 3
, точки остановки обозначены знаком “
×
”)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 2
39

















