
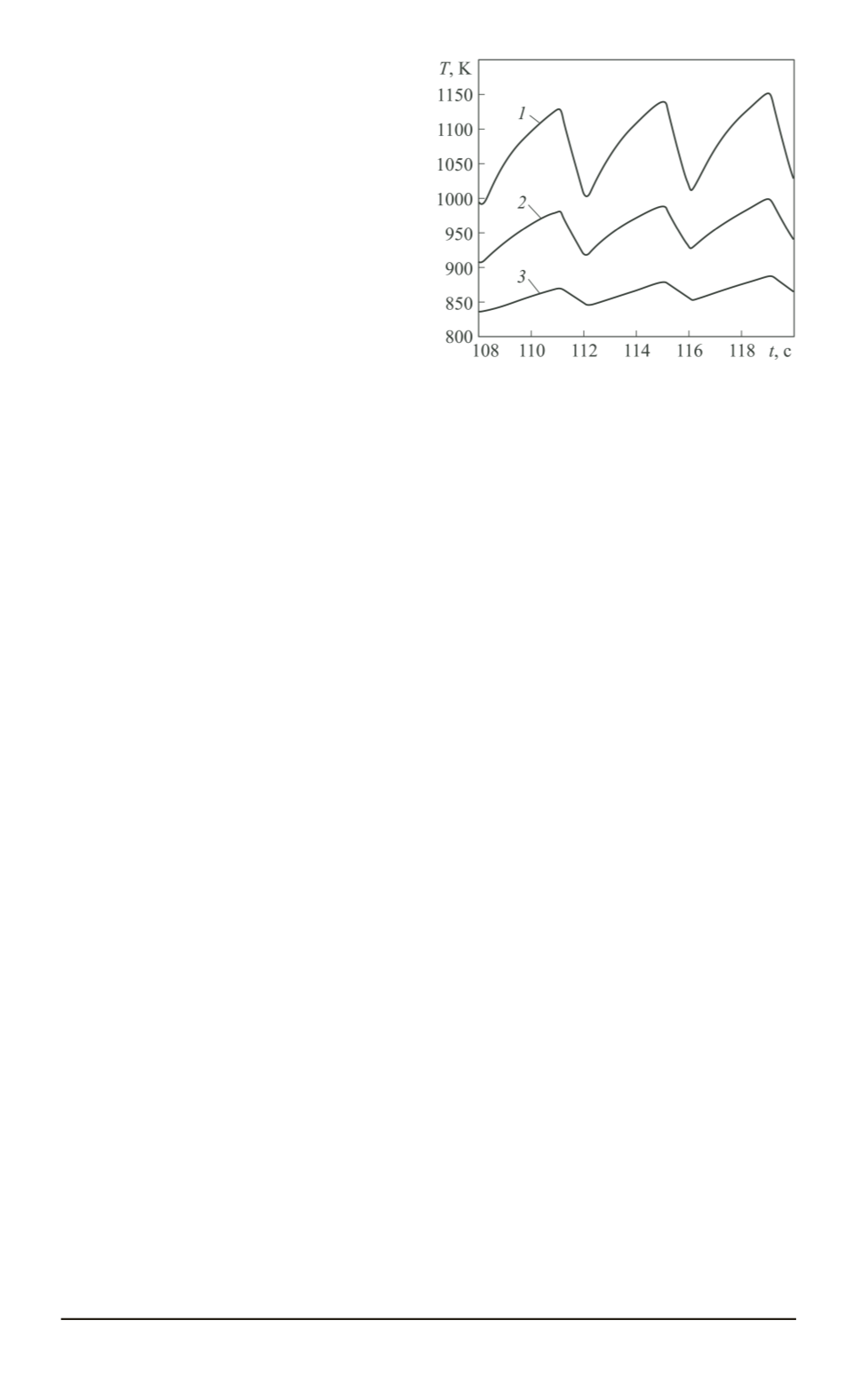
Рис. 3. Зависимость температуры в
сечении цилиндра
z
=
h/
2
от време-
ни при различных значениях
r
в кон-
це процесса разогрева:
1
—
T
(0
, h/
2
, t
)
;
2
—
T
(
r
0
/
2
, h/
2
, t
)
;
3
—
T
(3
r
0
/
4
, h/
2
, t
)
ρ
= 7780
кг/м
3
;
R
= 50
∙
10
−
3
м;
h
= 4
∙
10
−
3
м;
r
0
= 10
∙
10
−
3
м;
q
0
1
=
q
0
2
= 10
6
Bт/м
2
;
Δ
t
= 4
c;
t
0
= 3
c;
T
0
= 300
K;
ε
= 0
,
8
;
σ
= 5
,
67
×
×
10
−
8
Bт/(м
2
∙
K
4
).
Значения коэффициента теплопроводности и удельной теплоемко-
сти материала цилиндра в зависимости от температуры приведены
ниже [24]:
T
, K . . . . . . . . . . . . . . . . . . . . . . . . . . . 300 400 600 800 1000 1200 1400 1600
λ
, Bт/(м
∙
K
) . . . . . . . . . . . . . . . . . . . . . 48 47 41 37 32 23 21 20
c
, Дж/(кг
∙
K
) . . . . . . . . . . . . . . . . . . . . 470 505 520 660 615 580 560 545
Зависимость температуры в сечении цилиндра
z
=
h/
2
от време-
ни при различных значениях
r
в конце процесса разогрева
(108
≤
t
≤
≤
120)
показана на рис. 3. Синхронное внешнее периодическое воздей-
ствие двумя источниками теплоты на торцевые поверхности цилиндра
приводит к возникновению колебаний температуры в указанных точ-
ках с периодом, равным периоду воздействия источников теплоты, и
амплитудой, уменьшающейся при удалении точек от оси цилиндра.
Заключение.
Предложенный в работе алгоритм расчета нестаци-
онарного температурного поля в цилиндрическом теле учитывает из-
менение теплофизических свойств материала в зависимости от темпе-
ратуры, нелинейность граничных условий, позволяет задавать различ-
ные режимы внешнего теплового воздействия и условия теплообмена.
Алгоритм применим для решения задач об исследовании теплового
состояния цилиндрических тел при лазерной обработке.
ЛИТЕРАТУРА
1.
Карслоу Г.
,
Егер Д.
Теплопроводность твердых тел. М.: Наука, 1964. 488 с.
2.
Лыков А.В.
Теория теплопроводности. М.: Высш. шк., 1967. 600 с.
3.
Карташов Э.М.
Аналитические методы в теории теплопроводности твердых
тел. М.: Высш. шк., 2001. 550 с.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3
95

















