
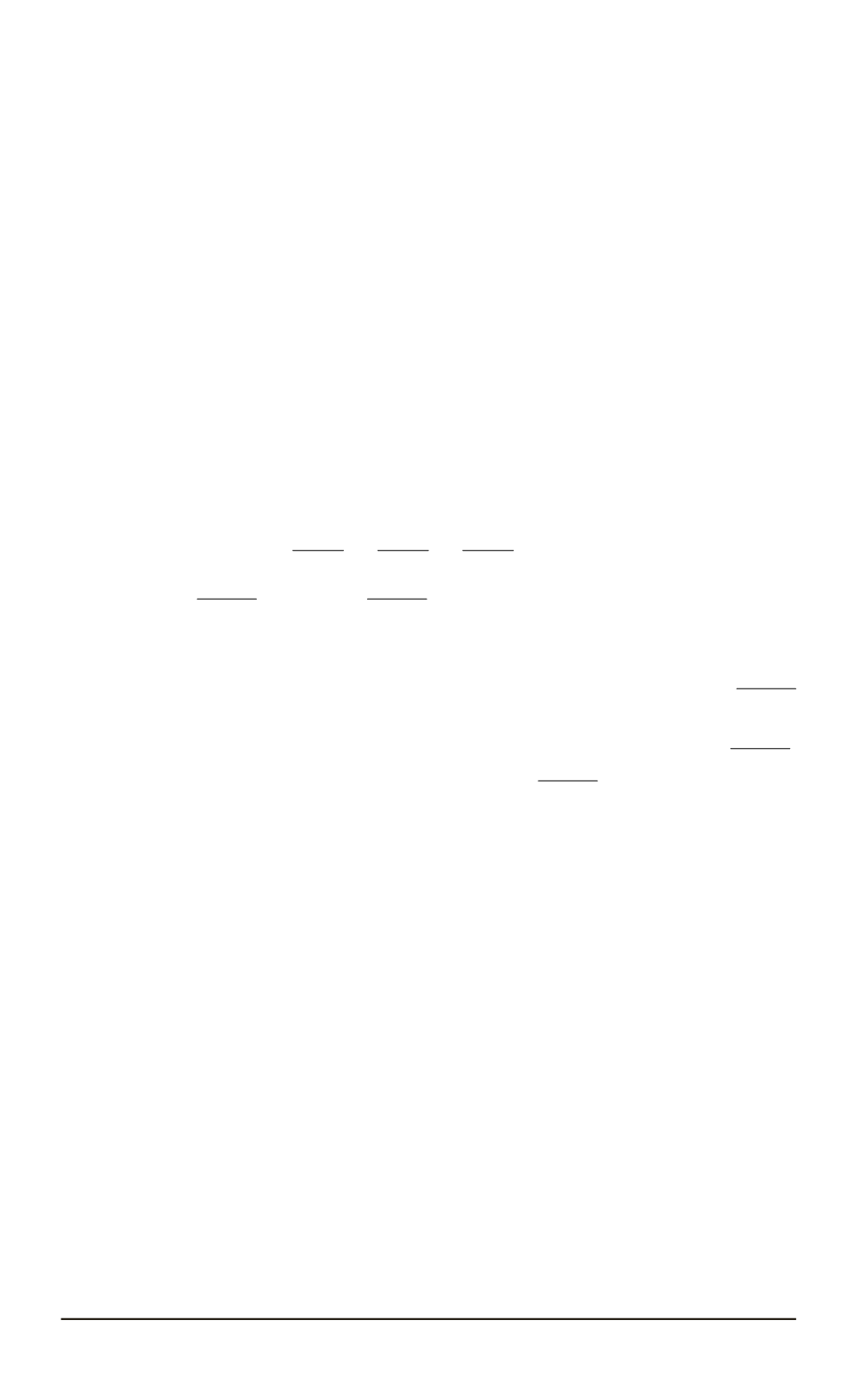
Согласно методу самосогласования, необходимо осредненные по
объему композита составляющие градиента температурного поля,
определяемые по формулам (7) и (8), приравнять нулю, т.е.
Δ
G
1
C
V
+
+ Δ
G
◦
1
(1
−
C
V
) = 0
, где
C
V
— объемная концентрация включений в
композите. Отсюда при обозначении
ˉ
λ
=
λ/λ
m
следует квадратное
уравнение
(1
−
D
0
1
−
(1
−
3
D
0
1
)
C
V
)Λ
2
1
−
(1
−
D
0
1
(1 + ˉ
λ
)
−
−
(1
−
3
D
0
1
ˉ
λ
)
C
V
)Λ
1
−
D
0
1
ˉ
λ
= 0
(9)
относительно
Λ
1
=
λ
∗
1
/λ
m
. Отметим, что уравнение (9) получено для
включений в форме приведенного эллипсоида и для его использова-
ния применительно к исходной форме включений необходимо найти
аналогичное уравнение для отношения
Λ
3
=
λ
∗
3
/λ
m
.
Уравнение (3) можно преобразовать не только к виду (5), но и к
виду
∂
2
T
∗
∂η
2
1
+
∂
2
T
∗
∂η
2
2
+
∂
2
T
∗
∂ξ
2
3
= 0
,
(10)
где
η
1
=
ξ
1
p
λ
∗
3
/λ
∗
1
;
η
2
=
ξ
2
p
λ
∗
3
/λ
∗
1
. Уравнение (10) описывает распре-
деление температуры в однородной изотропной среде с коэффициен-
том теплопроводности
λ
∗
3
. Такое преобразование равносильно измене-
нию масштаба в направлении координатных осей
Oξ
1
и
ξ
2
в
p
λ
∗
3
/λ
∗
1
раз. Это приведет к изменению длины полуосей
b
1
=
b
2
исходного эл-
липсоида вращения, которые теперь примут значение
b
0
1
=
b
1
p
λ
∗
3
/λ
∗
1
.
При этом отношение
ˉ
b
∗
=
b
3
/b
0
1
= (
b
3
/b
1
)
p
λ
∗
1
/λ
∗
3
для приведенного
эллипсоида вращения не изменит своего значения. Задав в изотропной
среде, описываемой уравнением (10), невозмущенное температурное
поле
T
∗
(
ξ
3
) =
G
3
ξ
3
и выполнив аналогичные проведенным выше пре-
образования, получим квадратное уравнение
(1
−
D
0
3
−
(1
−
3
D
0
3
)
C
V
)Λ
2
3
−
−
(1
−
D
0
3
(1 + ˉ
λ
)
−
(1
−
3
D
0
3
ˉ
λ
)
C
V
)Λ
3
−
D
0
3
ˉ
λ
= 0
.
(11)
В частном случае
ˉ
b
∗
= 1
, когда приведенный эллипсоид вырожда-
ется в шар, уравнения (9) и (11) при
D
0
1
=
D
0
3
= 1
/
3
совпадают между
собой и с квадратным уравнением
2Λ
2
−
(2
−
ˉ
λ
−
1+3( ˉ
λ
−
1)
C
V
)Λ
−
ˉ
λ
= 0
,
полученным методом самосогласования в работе [9] для изотропного
композита с шаровыми включениями. В этом случае
Λ
1
= Λ
3
= Λ
и отпадает необходимость рассмотрения приведенной формы включе-
ния.
При заданных значениях
b
1
=
b
2
и
b
3
полуосей эллипсоида враще-
ния, отношения
ˉ
λ
=
λ/λ
m
и объемной концентрации
C
V
включений
104
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 3

















