Так, для жидкого криптона вблизи температуры плавления (
T
пл
=
= 115
,
76
K)
ˉ
Z
≈
10
. Этому среднему значению сопутствуют два рав-
новероятных кластера с числом частиц
Z
0
≈
3
,
Z
00
≈
15
. Следователь-
но, набор “магических” чисел для криптона при
T
=
T
пл
представлен
следующим рядом: 2, 3, 10, 15. При
T
= 0
,
5 (
T
c
+
T
пл
)
, где
T
c
= 209
K,
ряд будет 2, 7, 10. При
T
=
T
c
ряд будет 1, 2, 2.(6), 3.
2. Прогнозирование частот ИК-спектров жидкостей.
Исследо-
вания спектров жидкостей в ИК-области показывают, что появление
спектральных линий связано с наличием вращательных и либрацион-
ных движений в структуре кластеров. Чем больше частиц содержится
в кластере, тем б´ольшая частота соответствует этому кластеру в ИК-
спектре.
В рамках теории эффективного поля вращательная энергия димера
в кластере совпадает с эффективной энергией, приходящейся на одну
частицу:
J
дим
ω
2
2
=
Z
2
ε
эфф
,
(16)
где
ε
эфф
— глубина потенциальной ямы эффективного потенциала вза-
имодействия;
J
дим
— момент инерции димера в кластере.
Эффективный потенциал взаимодействия
ϕ
эфф
(
r
)
отражает учет
трех- и многочастичных взаимодействий в конденсированной среде
и связан с парным потенциалом взаимодействия
ϕ
(
r
)
соотношением
[8, 9]
ϕ
эфф
(
r
) =
ϕ
(
r
)
−
kT ρE ,
(17)
где
E
— первая трех- или многочастичная элементарная функция
диаграммы;
k
— постоянная Больцмана.
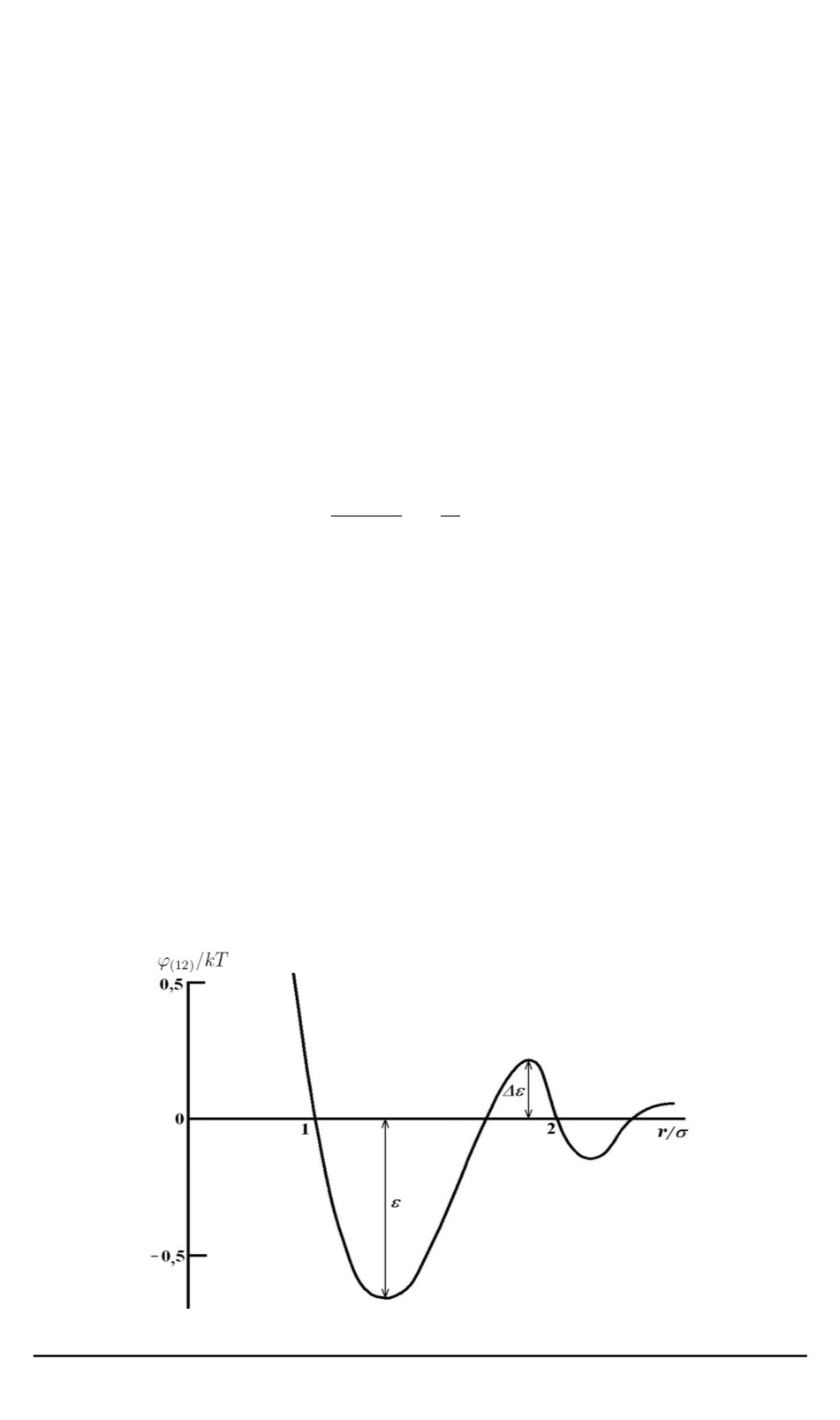
Глубина потенциальной ямы в эффективном потенциале взаимо-
действия (рис. 2) в общем случае определяется формулой
ε
эфф
=
ε
+ Δ
ε,
(18)
Рис. 2. Эффективный потенциал жидкого аргона, выраженный в единицах
kT
114
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3


