=
(10
,
−
20(
x
2
−
0
,
5)
,
20(
x
1
−
0
,
5)
,
0
,
1
,
5
,
0
,
0)
,
0
< r <
0
,
1
,
(1 + 9
f
(
r
)
,
−
20
f
(
r
)(
x
2
−
0
,
5)
,
20
f
(
r
)(
x
1
−
0
,
5)
,
1
,
5
,
0
,
0)
,
0
,
1
6
r <
0
,
115
,
(1
,
0
,
0
,
0
,
1
,
5
,
0
,
0)
, r
>
0
,
115
,
(5)
f
(
r
) = (0
,
115
−
r
)
/
0
,
015
, r
=
p
(
x
1
−
0
,
5)
2
+ (
x
2
−
0
,
5)
2
.
На границе области задано условие свободного вытекания веще-
ства. Показатель адиабаты
γ
= 5
/
3
, что соответствует идеальному
двухатомному газу, число Куранта
C
= 0
,
4
. Расчеты проведены на
треугольных сетках, содержащих
150 000
и
550 000
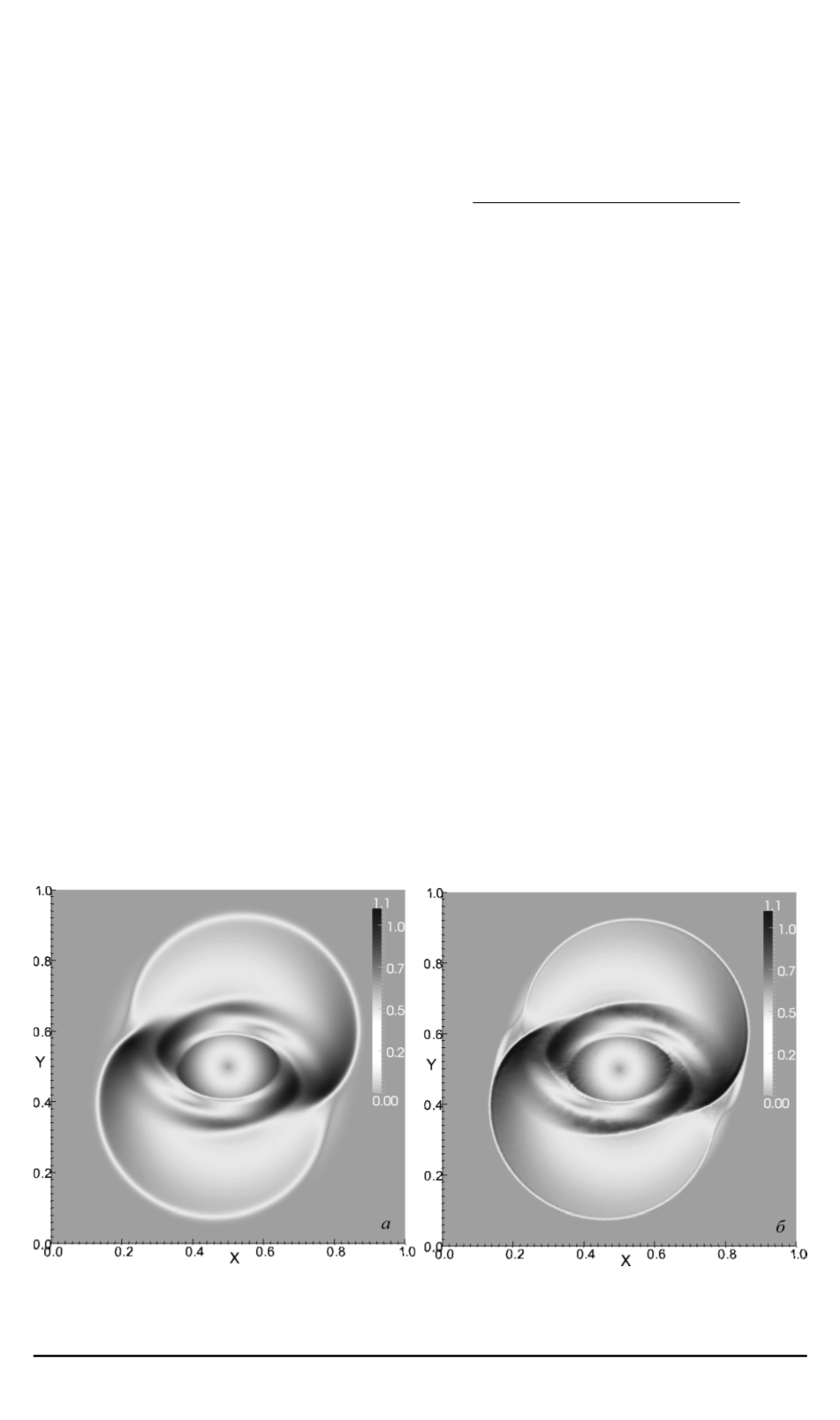
ячеек. На рис. 2
представлены распределения модуля вектора скорости в момент вре-
мени
t
= 0
,
15
, полученные разрывными методами Галеркина перво-
го и второго порядка точности с использованием численного потока
HLLD (для грубой сетки). Решение методом второго порядка приводит
к меньшему размытию разрывов как на внешней границе возмущен-
ного вещества, так и в области повышенной плотности.
На рис. 3 представлен график ускорения параллельной программы
при решении указанной задачи на учебно-экспериментальном вычи-
слительном кластере, а также графики линейного (идеального) уско-
рения и максимального ускорения согласно закону Амдала.
Доля параллельного кода в описанном алгоритме для подробной
сетки составляет 99,9%, что согласно закону Амдала ограничивает
ускорение величиной 31,2 на 32 ядрах. Решение задачи на одном ядре
занимает 234,3 мин, на 32 ядрах — 10,1 мин (ускорение в 23,2 раза).
Существенное расхождение реального ускорения с оценкой по зако-
ну Амдала объясняется главным образом не влиянием межмодульных
Рис. 2. Распределения модуля вектора скорости в задаче о вращении цилиндра,
полученные методами RKDG первого (
а
) и второго (
б
) порядков
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 4


