
В.С. Зарубин, О.В. Новожилова, С.И. Шишкина
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 1
23
=(1 )(1/(1 ) (5/2)/(4 5 )),
W
44
55
66
= = =15(1 )/(4 5 ).
W W W
Ос-
тальные элементы этой матрицы, которая также является блочной, равны нулю.
Следовательно, компоненты тензоров, обратных тензорам Эшелби для во-
локон и частиц матрицы композита, удалось представить элементами соответ-
ствующих блочных матриц. Поэтому вычисление инвариантов тензоров в ра-
венствах (5) целесообразно также вести в матричном виде.
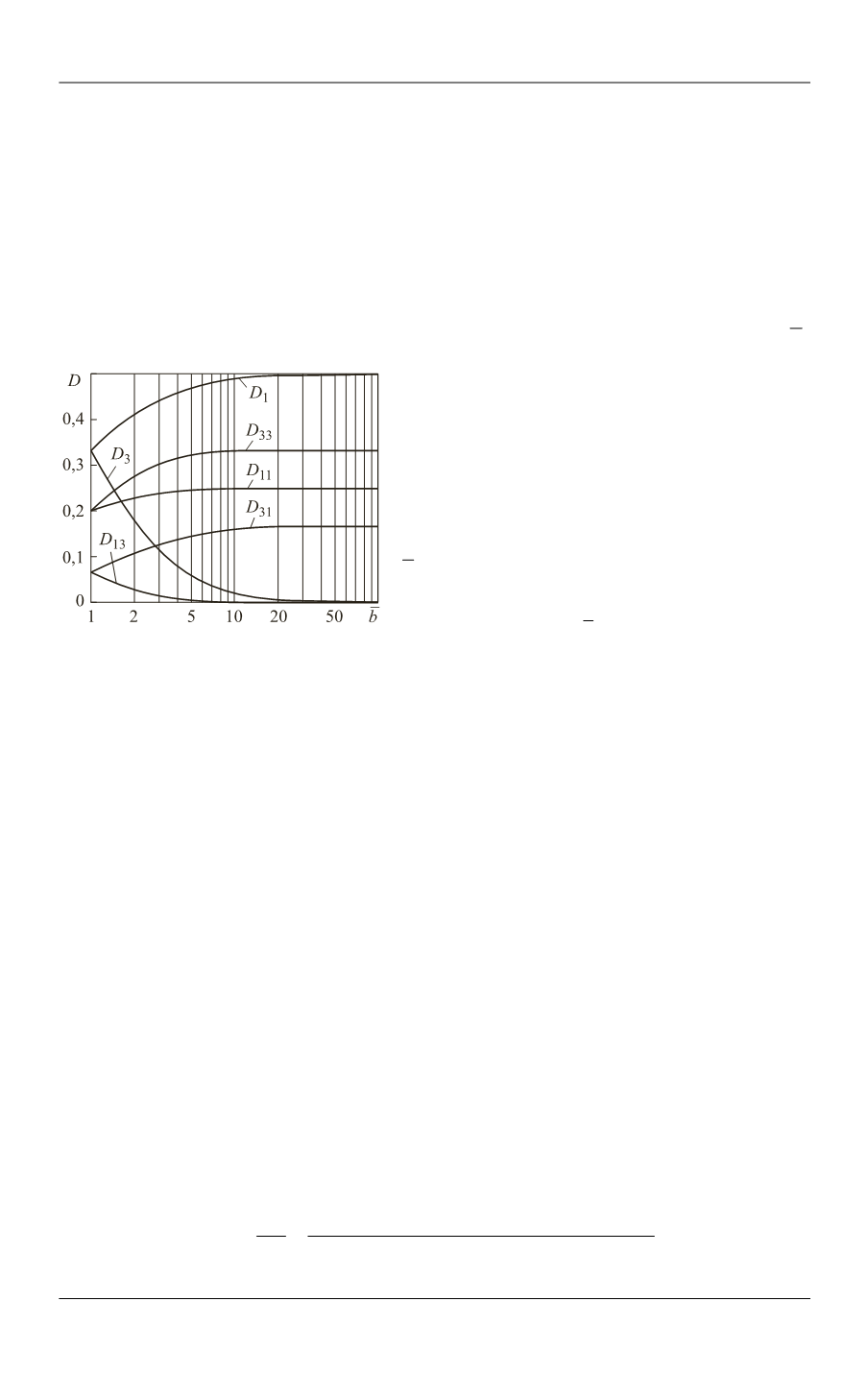
Количественный анализ математической модели.
Оценку в первом при-
ближении влияния удлинения волокон на упругие характеристики рассматри-
ваемых композитов можно получить, построив зависимости от параметра
b
коэффициентов
,
D
входящих в соотноше-
ния для элементов матрицы
,
N
соответ-
ствующей тензору Эшелби. В соответствии
с зависимостями, приведенными на рис. 1 в
полулогарифмических координатах, влия-
ние удлинения на значения указанных ко-
эффициентов пренебрежимо мало при
>100,
b
но с достаточной для оценочных
расчетов точностью это влияние можно не
учитывать уже при
>20.
b
Для количественного анализа совмест-
ного влияния на упругие свойства компо-
зита объемной концентрации
V
C
волокон
и других определяющих параметров следует
расширить область представления в графическом виде вычисляемых значений
объемного модуля
K
и модуля сдвига
.
G
Отметим, что по этим значениям при
необходимости можно вычислить не только коэффициент Пуассона
компо-
зита (формула приведена выше), но и его модуль Юнга
= 9 / (3
).
E KG K G
Для расширения области представления результатов расчетов используем
верхние и нижние оценки объемного модуля и модуля сдвига композита в виде
=(1 )
,
V
V
K C K C K
1/ =(1 )/
/
V
V
K C K C K
и
=(1 )
,
V
V
G C G C G
1/ =(1 )/
/ ,
V
V
G C G C G
следующие из теории смесей [19, 20] и более строго
обоснованные с привлечением двойственной вариационной формулировки за-
дачи о напряженно-деформированном состоянии неоднородного линейно
упругого тела [13]. Тогда при нормировании вычисляемых значений объемного
модуля по значению
K
в виде
= /
K K K
область графического представления
результатов расчетов этого модуля будет ограничена в положительном единич-
ном квадранте с координатами
V
C
и
K
сверху ординатой
=1,
K
а снизу — кри-
вой, построенной по формуле
1
= =
.
(1 ( /
1))(1 ( /
1))
V
V
K K
K
C K K
C K K
Рис. 1.
Зависимости коэффициентов,
определяющих компоненты тензора
Эшелби, от удлинения волокна
















