
М.П. Галанин, П.В. Глизнуцина, В.В. Лукин, А.С. Родин
44
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
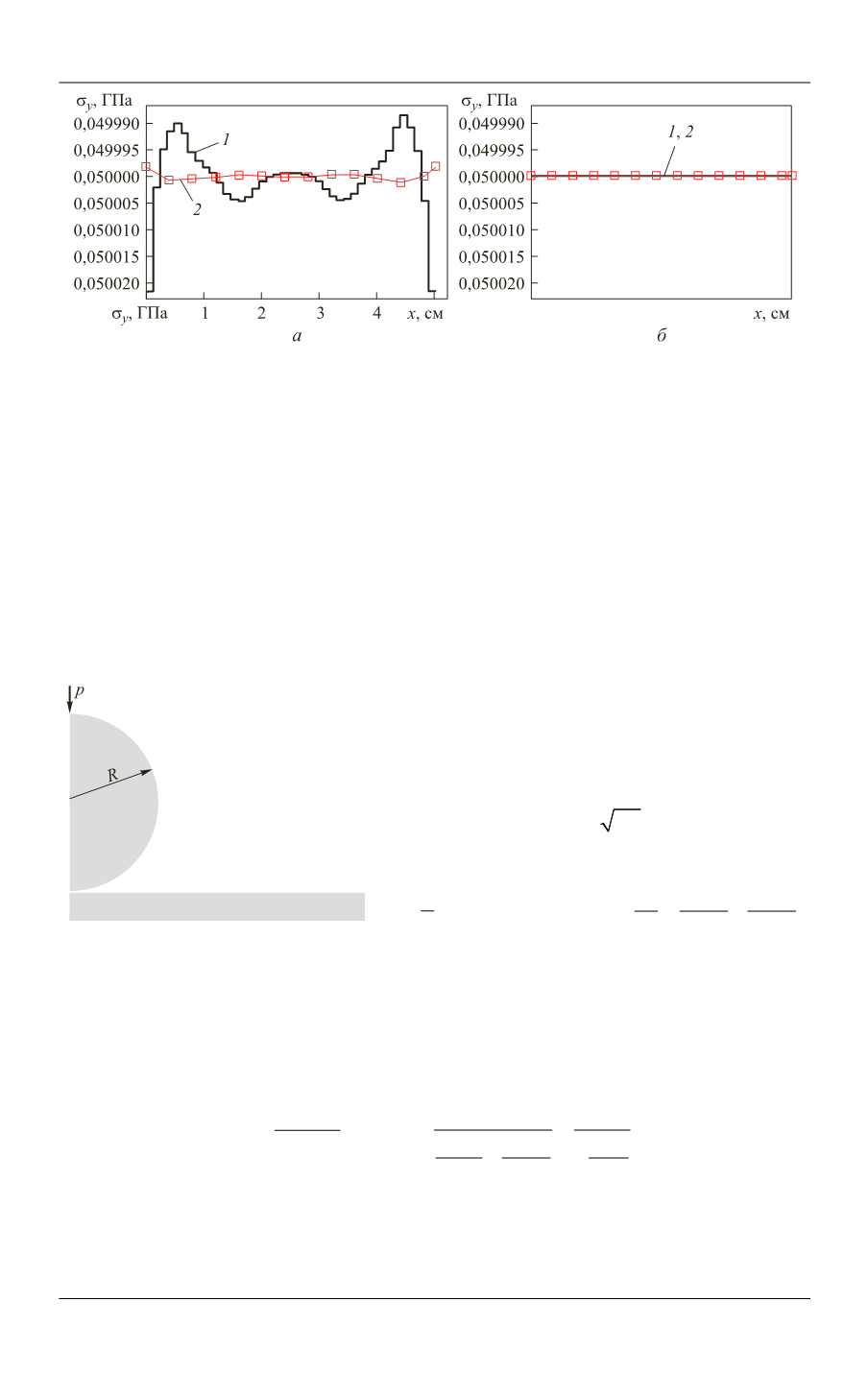
Рис. 8.
Зависимость вертикальной компоненты напряжений от координаты
x
, получен-
ная методами контакт точка–поверхность (
а
), контакт поверхность–поверхность с сег-
ментами (
б
):
1
,
2
— распределения соответствующей величины вдоль границы контакта для первого и
второго тел
Для сравнения численного решения с известным аналитическим рассмот-
рим
задачу Герца
(рис. 9, рис. 10). Параметры задачи приведены ниже:
Твердый шар радиусом
R
под влиянием
силы
p
вдавливается в упругое полупро-
странство на глубину
d
, при этом образуется
область контакта с полушириной
.
a Rd
(4)
Тогда силу можно рассчитать по формуле
* 1/2 3/2
4
,
3
p E R d
причем
2
2
1
2
*
1
2
1 1
1 ,
E E E
где
1
,
E
2
E
— модули упругости обоих тел;
1
,
2
— коэффициенты Пуассона.
Для рассматриваемой задачи аналитиче-
ская полуширина контакта будет определяться по формуле (4) с учетом того,
что
2/3
* 1/2
3
;
4
p
d
E R
*
1
2
1
2
1
1 .
1
1
12
E
E E
E
Подставив приведенные выше значения в указанные формулы, вычислим
*
E
= 3695,45 МПа,
d
= 0,19 см, а также по формуле (4) —
а
= 1,06 см.
R
, см
E
, ГПа
p
, МПа
60
0,23
7000
100
Рис. 9.
Схема системы цилиндр–
полуплоскость
















