Сравнение вариантов метода множителей Лагранжа для решения двумерных контактных задач

ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5

В исходной конфигурации сетки для двух тел совпадают на контактной по-

верхности. После деформирования они смещаются относительно друг друга. Оба

тела сжимаются в вертикальном направлении и расширяются в горизонтальном.

В силу геометрии задачи вертикальные компоненты перемещений и напряже-

ний на контактной поверхности близки к соответствующим нормальным компо-

нентам перемещений и напряжений. В угловой точке в аналитическом решении

имеют место бесконечные нормальные напряжения. С уменьшением шага числен-

но получаемые значения нормальных напряжений возрастают по модулю.

Различие в данных, получаемых двумя первыми методами, невелико — в

пятом знаке после запятой (0,1 %). Однако можно отметить, что второй метод

лучше отражает физические свойства задачи, чем первый, так как он позволяет

получать значения нормальных напряжений в угловой точке более близкими к

«аналитической бесконечности».

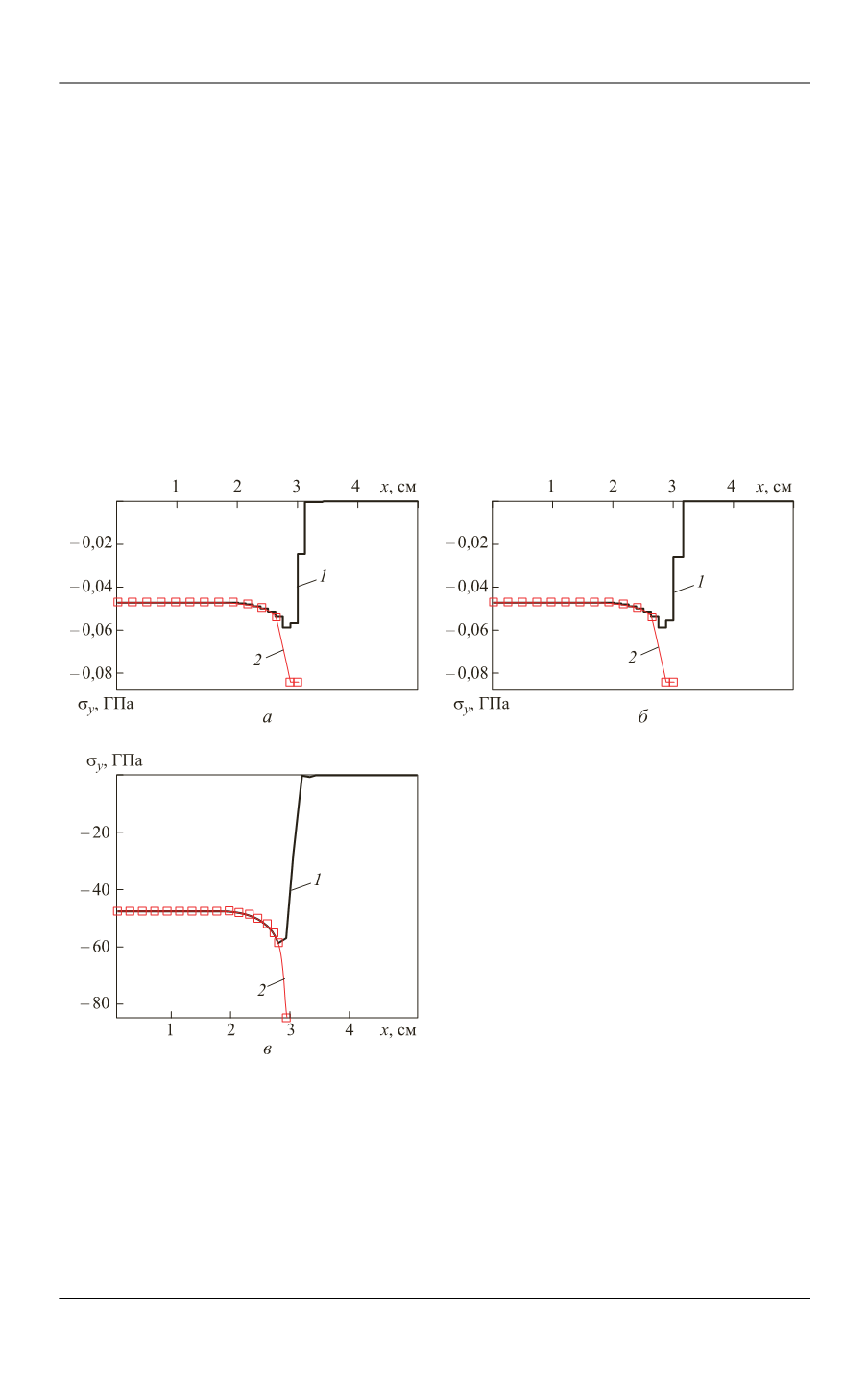
Результаты, полученные использованием обоих методов, близки к резуль-

татам, полученным с помощью альтернирующего метода Шварца. Поскольку

наиболее интересным представляется распределение нормальных напряжений,

то на рис. 4 приведены полученные в расчетах с шагом

= 0,125

распределения

компоненты напряжений



которая в силу геометрии близка к нормальной

компоненте.

Рис. 4.

Зависимость вертикальной ком-

поненты напряжений от координаты

полученная методами контакт точка–

поверхность (

), контакт поверхность–

поверхность (

) и альтернирующим ме-

тодомШварца (

) при шаге 0,125 см:

— распределения соответствующей ве-

личины вдоль границы контакта для пер-

вого и второго тел