
Сравнение вариантов метода множителей Лагранжа для решения двумерных контактных задач
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
43
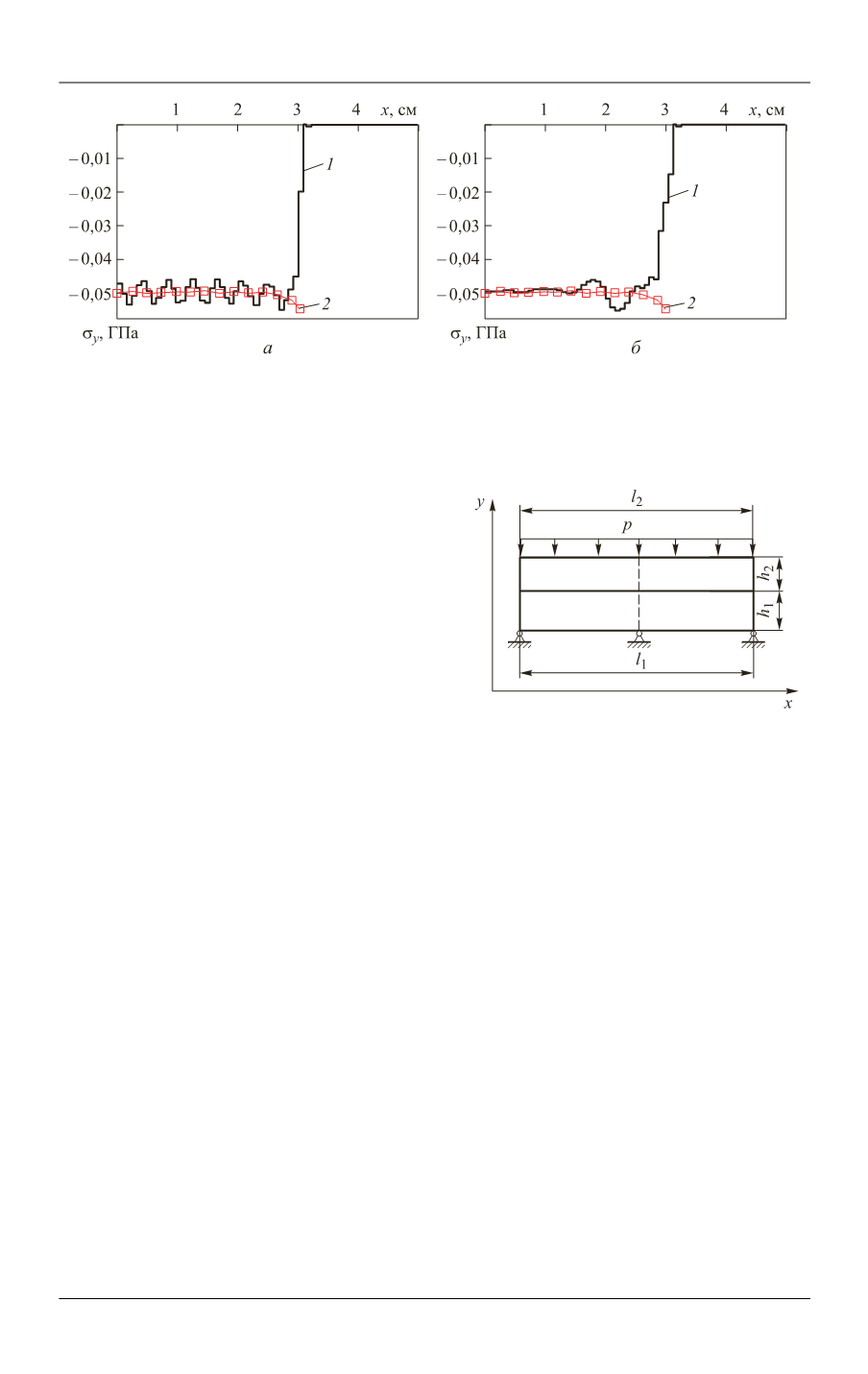
Рис. 6.
Зависимость вертикальной компоненты напряжений от координаты
x
, полу-
ченная методами контакт точка–поверхность (
а
), контакт поверхность–поверхность (
б
):
1
,
2
— распределения соответствующей величины вдоль границы контакта для первого и
второго тел
Для того чтобы показать различие ме-
тодов контакт поверхность–поверхность и
контакт поверхность–поверхность с под-
сегментами проведем тестовый расчет для
задачи, аналогичной первой, только с оди-
наковой геометрией брусков —
задачи об
одинаковых брусках из разных материалов с
неравномерной сеткой
(рис. 7). Первый
брусок лежит на гладкой поверхности, вто-
рой — на первом. Сверху ко второму бруску
приложена распределенная сила
.
p
Анало-
гично рассмотрим лишь половину области с
соответствующими закреплениями. Параметры задачи приведены ниже:
l
1
, см
l
2
, см
h
1
, см
h
2
, см
1
2
E
1
, ГПа
E
2
, ГПа
p
, МПа
10
10
3
3
0,3
0,3
700
70
50
Рассмотрим эту задачу при несовпадении сеток на контактной поверхности.
Шаг сетки для первого тела примем равным 0,12 см, шаг сетки для второго —
0,15 см. Получаемые напряжения приведены на рис. 8. Черным цветом показано
распределение соответствующей величины на контактной поверхности для
первого тела, красным — распределение соответствующей величины на кон-
тактной поверхности для второго тела.
Аналитическое решение задачи для вертикальной компоненты напряжений:
.
y
p
Как видно на рисунках, в решении метода контакт поверхность–
поверхность наблюдаются колебания, однако они малы — в пятом знаке после
запятой. В решении метода контакт поверхность–поверхность с подсегментами
колебания отсутствуют, а полученные результаты очень близки к аналитическому
решению.
Рис. 7.
Схема системы из двух брусков
для задачи об одинаковых брусках из
разных материалов с неравномерной
сеткой
















