
Сравнение вариантов метода множителей Лагранжа для решения двумерных контактных задач
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
39
2.
Метод контакт поверхность–поверхность
.
c
c
N N
Тогда (3) можно
записать в виде
( )
( )
т
( )
( )
( )
.
C
m
s
C
c c
s
m
W
N N x N x d
В этом случае для интегрирования используют квадратурную формулу
Гаусса с четырьмя точками интегрирования на сегменте граничного элемента
активного тела.
3.
Метод контакт поверхность–поверхность с подсегментами
имеет одно
отличие от предыдущего метода: сегменты активного тела, по которому идет
интегрирование, разбиваются на подсегменты так, чтобы каждому подсегменту
активного тела при вычислении интеграла соответствовал лишь один сегмент
пассивного тела.
В таком случае интегрирование идет по сегменту активного тела и осу-
ществляется более точно, чем в предыдущем методе. Тогда (3) можно записать в
виде
( )
( )
т
,
C
m
s
m
s
C
c
c
c
m
W
G x G x d
где
( ) ( ) ;
( ) ( ) ;
C
C
m
s
c
c
c
s
c
G N N d I G N N d I
I
— единичная матрица.
Результаты тестовых расчетов.
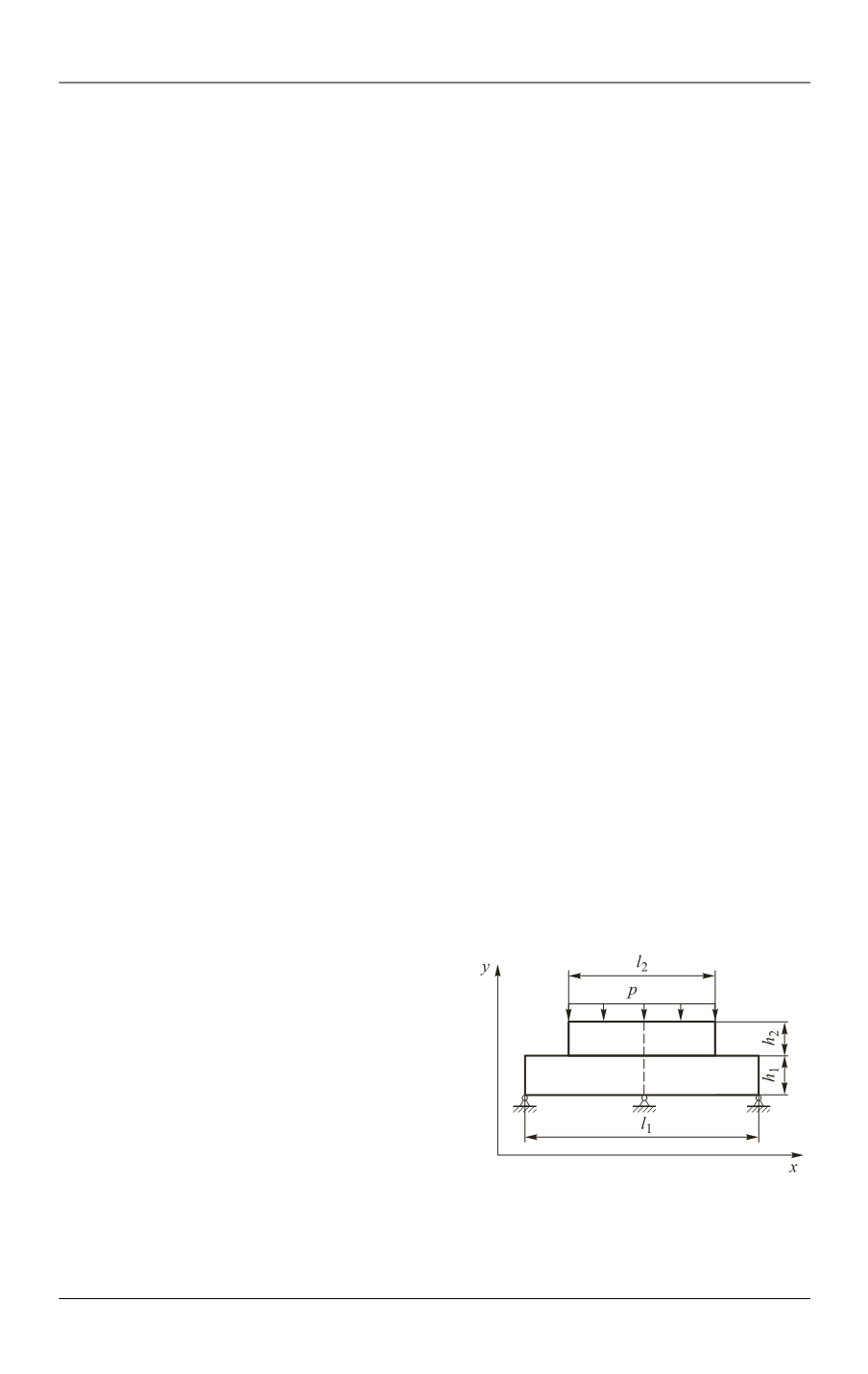
В качестве тестовой решим
задачу о двух
брусках из одинакового материала
(рис. 2). Первый брусок лежит на гладкой
поверхности, второй — на первом. Сверху ко второму бруску приложена рас-
пределенная сила
.
p
Параметры задачи приведены ниже:
1
,
l
см
2
,
l
см
1
,
h
см
2
,
h
см
1
2
1
,
E
ГПа
2
,
E
ГПа
,
p
МПа
10 6 3 3 0,3 0,3 70 70 50
В силу симметрии задачи рассмотрим половину области. В таком случае за-
крепим ось симметрии системы брусков по координате
x
на левой границе, пер-
вый брусок по координате
y
на нижней
границе и ко второму бруску сверху при-
ложим распределенную нагрузку.
Рассмотрим решение задачи двумя ме-
тодами — контакт точка–поверхность и
контакт поверхность–поверхность, а так-
же сравним с получаемым численным ре-
шением, найденным с помощью альтерни-
рующего метода Шварца [7].
Распределения компоненты перемеще-
ний
y
u
и компоненты напряжений
y
для
расчетов с шагом
0,125
h
см приведены
Рис. 2.
Схема системы из двух брусков
для задачи о двух брусках из одинако-
вого материала
















