
М.П. Галанин, П.В. Глизнуцина, В.В. Лукин, А.С. Родин
42
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
Вертикальные перемещения и напряжения на контактной поверхности у
обоих тел близки друг к другу, следовательно, близки нормальные перемещения
и напряжения. При этом решение имеет особенность в угловой точке верхнего
тела.
Рассмотрим эту задачу при несовпадении сеток на контактной поверхности.
Шаг сетки для первого тела примем равным 0,08 см, шаг сетки для второго тела —
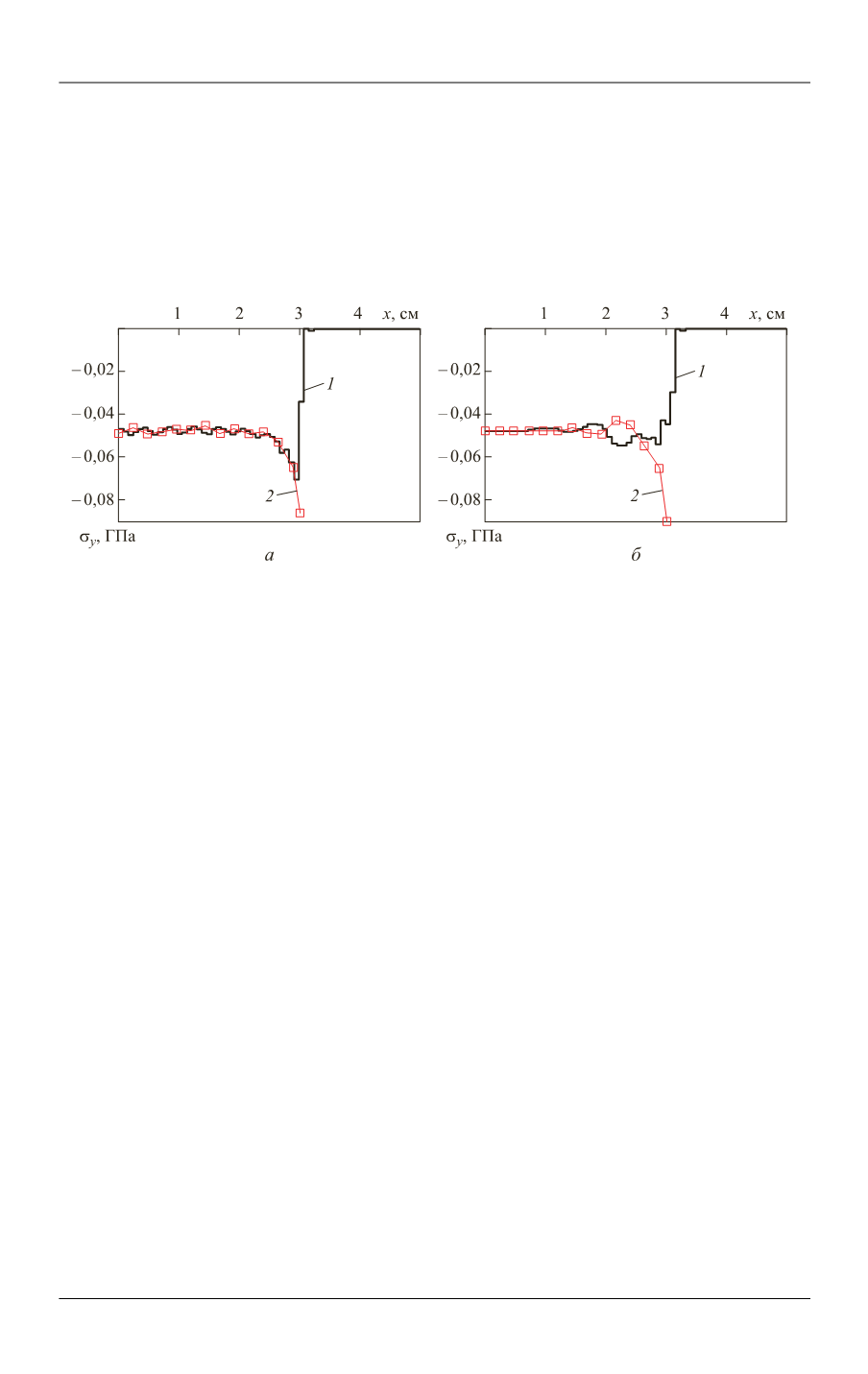
0,1 см. Получаемые напряжения приведены на рис. 5.
Рис. 5.
Зависимость вертикальной компоненты напряжений от координаты
x
, полученная
методами контакт точка–поверхность (
а
), контакт поверхность–поверхность (
б
):
1
,
2
— распределения соответствующей величины вдоль границы контакта для первого и
второго тел
Метод контакт точка–поверхность дает расхождение напряжений на всей
контактной поверхности, метод контакт поверхность–поверхность — практиче-
ское совпадение контактных напряжений первого и второго тел в центре систе-
мы брусков, однако ближе к угловой точке появляются колебания, причем их
амплитуда больше, чем в методе контакт точка–поверхность.
Рассмотрим аналогичную
задачу о двух брусках из разных материалов
с бо-
лее жестким первым телом. Параметры задачи приведены ниже:
l
1
, см
l
2
, см
h
1
, см
h
2
, см
1
2
E
1
, ГПа
E
2
, ГПа
p
, МПа
10
6
3
3
0,3
0,3
700
70
50
Аналогично предыдущей задаче рассмотрим половину области с соответ-
ствующими закреплениями.
Рассмотрим эту задачу при несовпадении сеток на контактной поверхности.
Шаг сетки для первого тела примем равным 0,08 см, шаг сетки для второго —
0,1 см. Получаемые напряжения приведены на рис. 6.
В распределениях, полученных методом контакт точка–поверхность,
наблюдаются колебания с приблизительно неизменной амплитудой на всей
контактной границе, а в распределениях, полученных методом контакт поверх-
ность–поверхность, ближе к центру симметрии задачи колебания несуществен-
ны, но в окрестности особой точки колебания возрастают и их амплитуда боль-
ше, чем в методе контакт точка–поверхность.
















