
М.П. Галанин, П.В. Глизнуцина, В.В. Лукин, А.С. Родин
36
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 5
В большинстве случаев численного анализа контактного взаимодействия
тел кинематические контактные условия можно учесть в явном виде, так как в
качестве неизвестных обычно выбираются перемещения, и соответствующее
условие переходит в условие равенства нормальных компонент перемещений на
контактной поверхности. Силовые контактные условия содержат производные
численного решения и могут быть выполнены только в некотором слабом
смысле — в виде равенства интегральных средних от нормальных напряжений
на контактной поверхности. Указанное обстоятельство не позволяет включать
данные условия, например, в дискретизованную систему уравнений метода ко-
нечных элементов (МКЭ) явным образом — это приведет к потере точности
численного решения. В этом случае для учета силовых условий приходится
применять дополнительные приемы.
Для решения контактных задач применяют ряд численных методов, среди ко-
торых метод множителей Лагранжа [3], метод штрафов [3], метод Шварца [4, 5]
и другие реже используемые (например, метод конечных элементов с использова-
нием функций формы Эрмита). Здесь рассмотрим применение метода множите-
лей Лагранжа, как одного из наиболее эффективных методов учета контактного
взаимодействия, при решении двумерных статических задач теории упругости для
системы тел.
Постановка контактной задачи и математическая модель.
Рассмотрим по-
становку двумерной контактной задачи [3, 6].
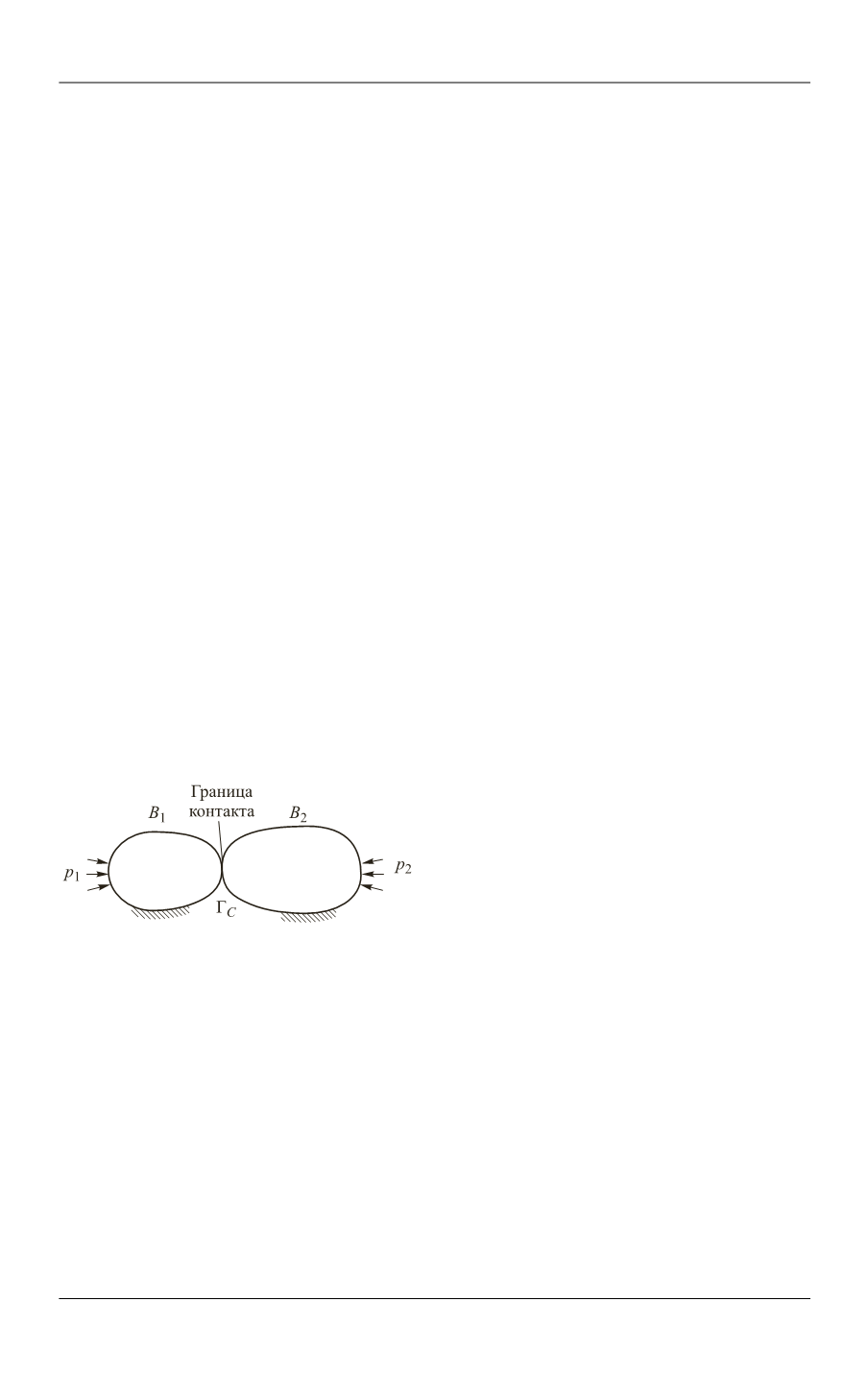
Пусть имеются два тела
1
B
и
2
,
B
которые в результате приложенных нагру-
зок вступают в контакт (рис. 1). На контактной поверхности
C
должны быть
выполнены условия непроникания одного тела в другое:
= min (
)
0,
,
g
x
x x n
x
где ,
— индексы контактирующих
тел;
— поверхность тела
,
B
обра-
щенная к поверхности тела
;
B
—
поверхность тела
,
B
обращенная к по-
верхности тела
;
B
n
— внешняя нор-
маль в точке
x
к поверхности контакта для тела
;
B
g
— зазор между точ-
кой
x
и телом
.
B
Контакт возникает тогда, когда хотя бы для одной точки
тела
B
зазор равен нулю. Если для всех точек тела
B
зазор положителен, то
тела не находятся в контакте.
В случае контакта на совместной границе контактирующих тел возникают
распределенные поверхностные силы, далее обозначаемые .
t
Нормальная и ка-
сательная составляющие распределенной контактной силы, действующей на
любое из тел, имеют вид
= 0;
n
t
t n
(1)
Рис. 1.
Схема контакта твердых тел
















