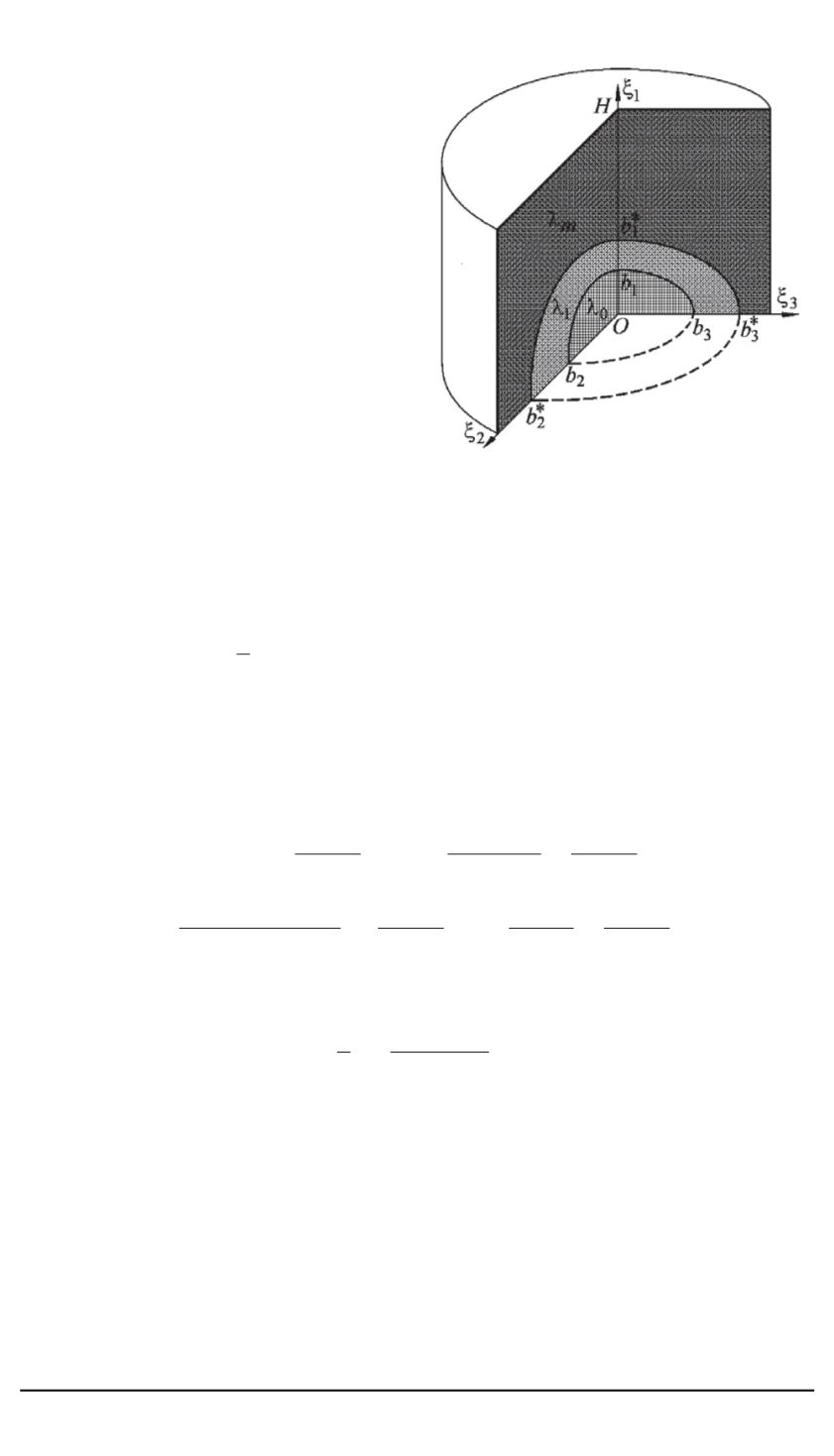
Рис. 1. Модель композита с эллипсои-
дальными включениями
Боковую поверхность цилин-
дра примем идеально теплоизоли-
рованной, температуру основания
при
ξ
1
= 0
положим равной ну-
лю, а на втором основании при
ξ
1
=
H
зададим температуру
T,
◦
1
H
.
Таким образом, в неоднородной
цилиндрической области объемом
V
0
=
HS
0
, ограниченной поверх-
ностью
S
, распределение темпера-
туры
T
(
M
)
и коэффициенттепло-
проводности
Λ(
M
)
являются функ-
циями координатточки
M
∈
V
,
причем функция
Λ(
M
)
кусочно по-
стоянна в каждой из подобластей
области
V
(см. рис. 1).
Примем в качестве допустимого для минимизируемого функцио-
нала [ 7 ]
J
[
T
] =
1
2
V
Λ(
M
)
∇
T
(
M
)
2
dV
(
M
)
, M
∈
V,
(14)
где
∇
— дифференциальный оператор Гамильтона, линейное по высо-
те цилиндра распределение температуры с постоянной составляющей
градиента
T,
◦
1
. Тогда из формулы (14) получим
J
1
[
T
] =
λ
1
(
T,
◦
1
)
2
2
HS
0
−
2
πb
∗
1
b
∗
2
b
∗
3
3
λ
1
(
T,
◦
1
)
2
2
+
+2
π
b
∗
1
b
∗
2
b
∗
3
−
b
1
b
2
b
3
3
λ
m
(
T,
◦
1
)
2
2
+ 2
π
b
1
b
2
b
3
3
λ
0
(
T,
◦
1
)
2
2
.
(15)
Для максимизируемого функционала [ 7 ]
I
[q] =
−
1
2
V
q(
M
)
2
Λ(
M
)
dV
(
M
)
−
−
S
T
(
P
)q(
P
)
·
n(
P
)
dS
(
P
)
, P
∈
S,
(16)
(
n
— единичный вектор внешней нормали к поверхности
S
) в качест ве
допустимого распределения вектора плотности теплового потока
q
примем постоянное значение
q
=
−
λ
1
T,
◦
1
единственной составляющей
этого вектора, перпендикулярной основаниям цилиндра. В этом случае
формула (16) приметвид
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 3
81


