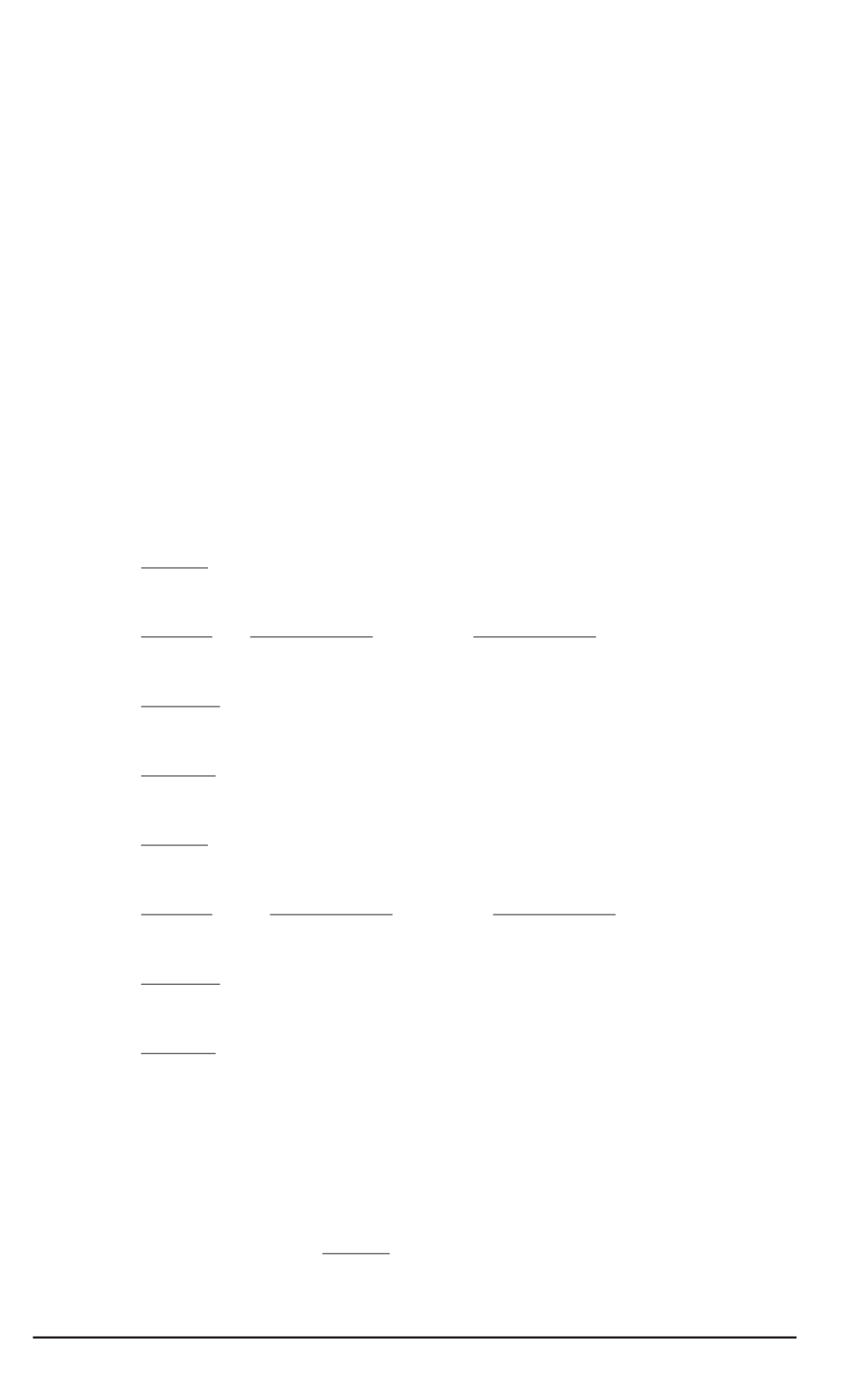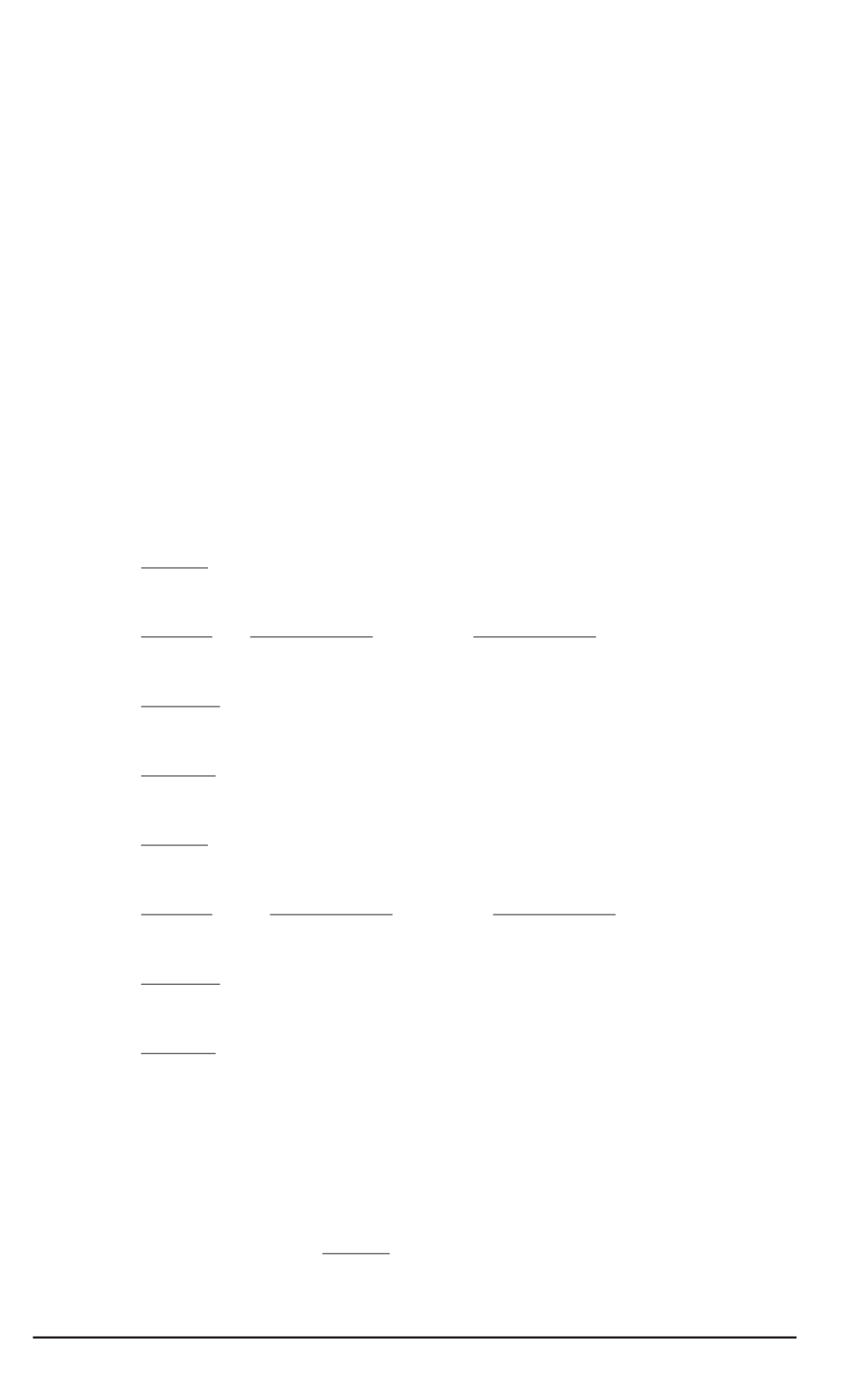
Здесь
y
j
(
ξ
j
, t
) =
Re
¯
y
j
(
ξ
j
, t
) =
Re
[(
y
1
j
(
ξ
j
) +
i y
2
j
(
ξ
j
))(cos
ωt
+
i
sin
ωt
)] =
=
Re
[
y
1
j
(
ξ
j
) cos
ωt
−
y
2
j
(
ξ
j
) sin
ωt
+
i
(
y
1
j
(
ξ
j
) sin
ωt
+
y
2
j
(
ξ
j
) cos
ωt
)] =
=
y
1
j
(
ξ
j
) cos
ωt
−
y
2
j
(
ξ
j
) sin
ωt.
Аналогично определяются выражения и для оставшихся функций,
в результате получим:
⎛
⎜⎜⎝
y
j
(
ξ
j
, t
)
ϕ
j
(
ξ
j
, t
)
M
j
(
ξ
j
, t
)
Q
j
(
ξ
j
, t
)
⎞
⎟⎟⎠
=
⎛
⎜⎜⎝
y
1
j
(
ξ
j
)
ϕ
1
j
(
ξ
j
)
M
1
j
(
ξ
j
)
Q
1
j
(
ξ
j
)
⎞
⎟⎟⎠
cos
ωt
−
⎛
⎜⎜⎝
y
2
j
(
ξ
j
)
ϕ
2
j
(
ξ
j
)
M
2
j
(
ξ
j
)
Q
2
j
(
ξ
j
)
⎞
⎟⎟⎠
sin
ωt
(в дальнейшем индексучастка
j
будет опущен).
После подстановки решения (4) в (3) и разделения переменных
получим систему дифференциальных уравнений
dy
1
(
ξ
)
dξ
=
lϕ
1
(
ξ
);
dϕ
1
(
ξ
)
dξ
=
l
EJ
(1 +
ν
2
)
M
1
(
ξ
) +
lν
EJ
(1 +
ν
2
)
M
2
(
ξ
);
dM
1
(
ξ
)
dξ
=
lQ
1
(
ξ
);
dQ
1
(
ξ
)
dξ
=
l
(
μω
2
−
k
)
y
1
(
ξ
) +
lαμωy
2
(
ξ
);
dy
2
(
ξ
)
dξ
=
lϕ
2
(
ξ
);
dϕ
2
(
ξ
)
dξ
=
−
lν
EJ
(1 +
ν
2
)
M
1
(
ξ
) +
l
EJ
(1 +
ν
2
)
M
2
(
ξ
);
dM
2
(
ξ
)
dξ
=
lQ
2
(
ξ
);
dQ
2
(
ξ
)
dξ
=
−
lαμωy
1
(
ξ
) +
l
(
μω
2
−
k
)
y
2
(
ξ
)
.
Введем вектор состояния сечения в виде
X
(
ξ
) = (
y
1
(
ξ
)
, ϕ
1
(
ξ
)
, M
1
(
ξ
)
, Q
1
(
ξ
)
, y
2
(
ξ
)
, ϕ
2
(
ξ
)
, M
2
(
ξ
)
, Q
2
(
ξ
))
T
.
(5)
В новых обозначениях система (5) запишется как
dX
(
ξ
)
dξ
=
AX
(
ξ
)
,
(6)
где
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 2