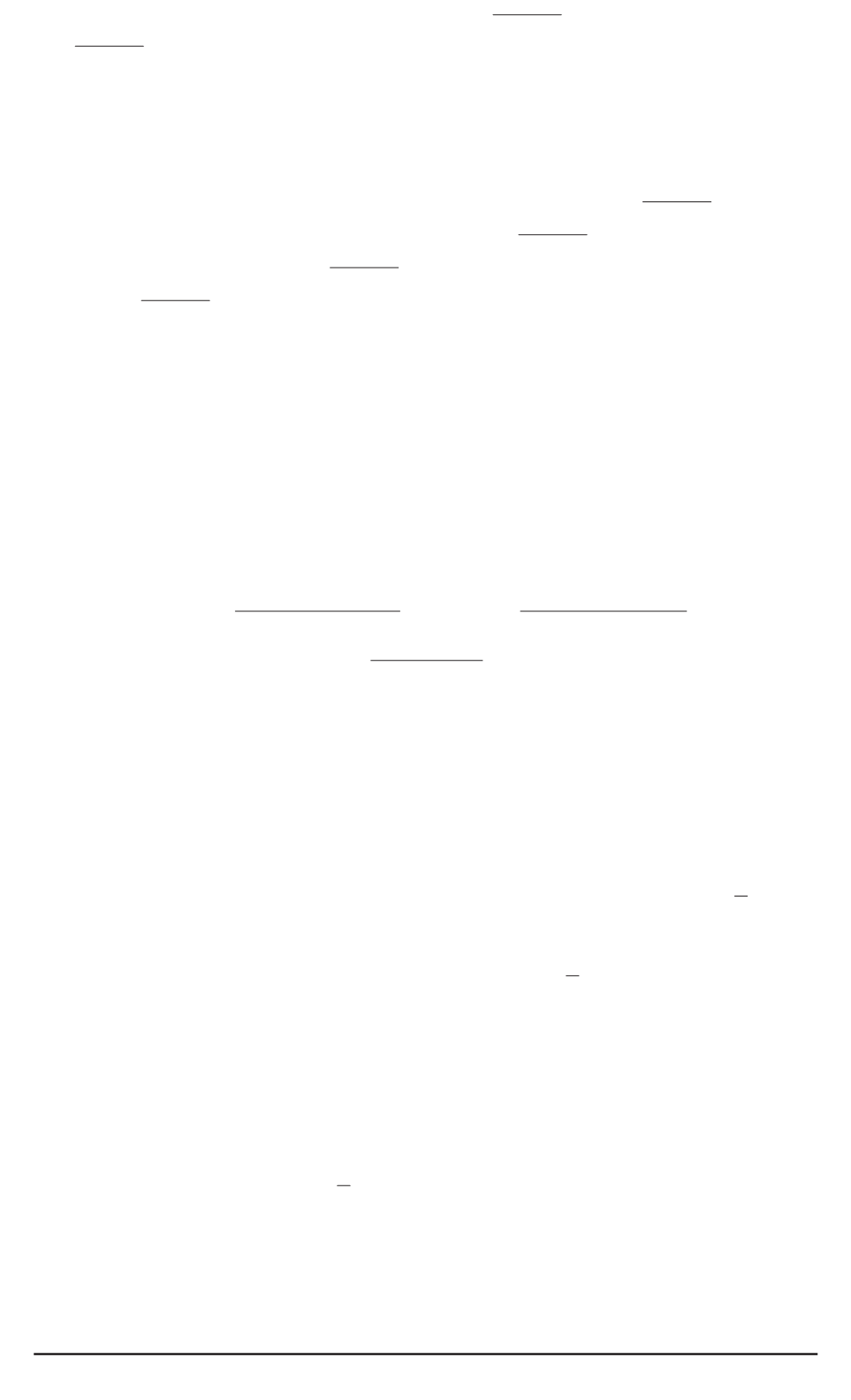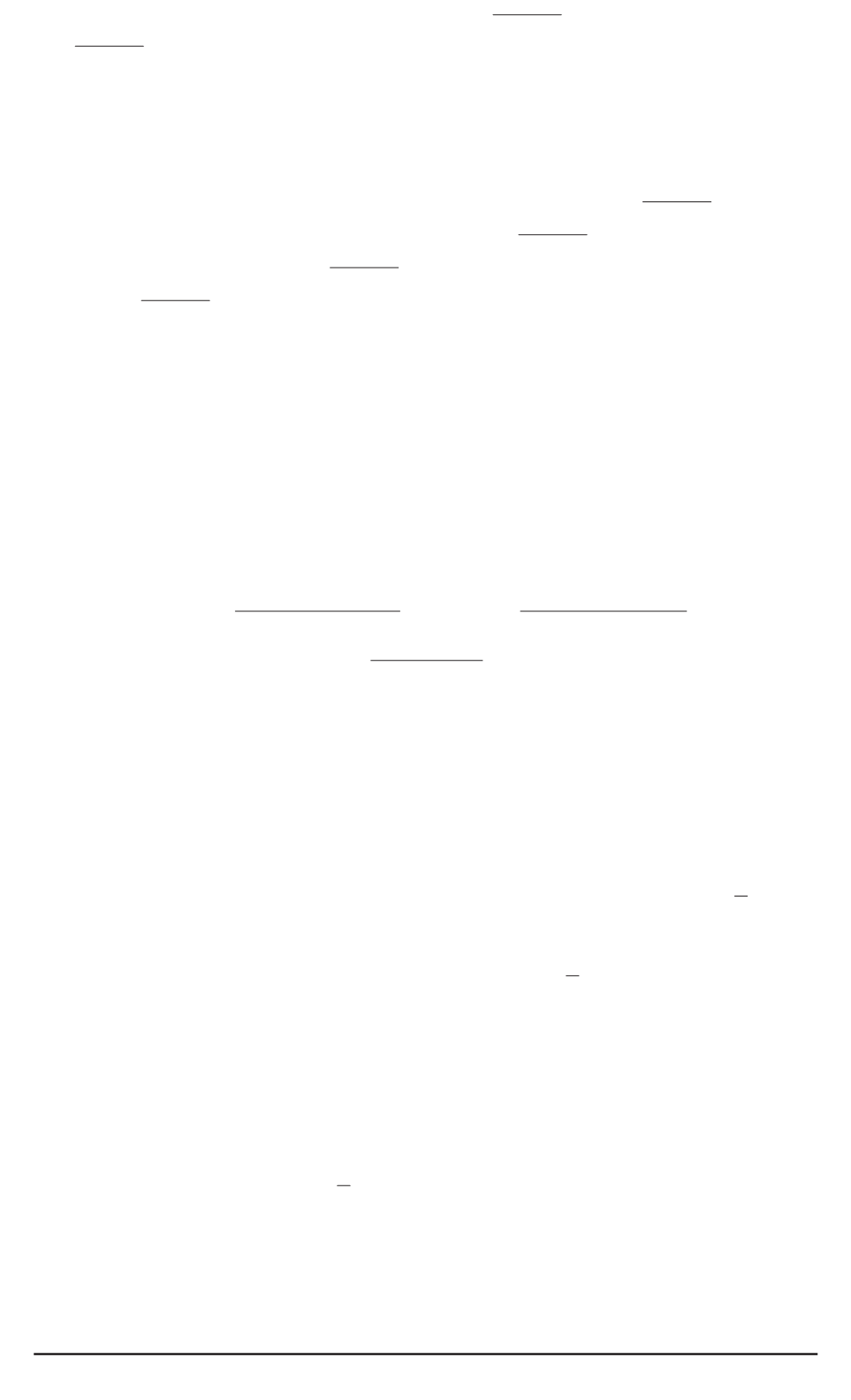
с нормализованными
|
Ψ
1
>
=
a
|
00
>
+ 1
−
a
2
|
11
>
и
Ψ
2
=
a
|
10
>
+
+
√
1
−
a
2
|
01
>
с
0
< a <
1
. Из (83) видно, что смешанность зависит
только от
q
, запутанность — от
q
и
a
. Формула (83) в развернутом виде
выглядит так:
ρ
AB
=
=
⎛
⎜⎜⎝
qa
2
0
0
qa
√
1
−
a
2
0
(1
−
q
)(1
−
a
2
) (1
−
q
)
a
√
1
−
a
2
0
0 (1
−
q
)
a
√
1
−
a
2
(1
−
q
)
a
2
0
qa
√
1
−
a
2
0
0
q
(1
−
a
2
)
⎞
⎟⎟⎠
.
(83a)
Отсюда
S
(
AB
) =
−
q
log
2
q
−
(1
−
q
) log
2
(1
−
q
)
,
(84)
S
(
A
) =
−
(
a
2
−
2
qa
2
+
q
) log
2
(
a
2
−
2
qa
2
+
q
)
−
−
(1
−
a
2
+ 2
qa
2
−
q
) log
2
(1
−
a
2
+ 2
qa
2
−
q
)
,
(85)
S
(
B
) =
−
a
2
log
2
a
2
−
(1
−
a
2
) log
2
(1
−
a
2
)
,
(86)
i
B
|
A
=
S
(
AB
)
−
S
(
A
)
S
(
B
)
, i
A
|
B
=
S
(
AB
)
−
S
(
B
)
S
(
A
)
,
(87)
C
= 2
a
2
(1
−
a
2
)
|
1
−
2
q
|
.
(88)
Всегда
S
(
A
)
S
(
AB
)
;
S
(
B
)
может быть как больше, так и меньше
S
(
AB
)
. Согласно определению [6] подсистема
А
почти всегда кванто-
вая, подсистема
В
может быть и квантовой и классической. На рис. 13
показанызависимости
i
B
|
A
,
С
и Tr
ρ
2
AB
от
q
и
a
2
, которые имеют ожи-
даемый вид. Нетривиальной является лишь зависимость
i
B
|
A
от
a
2
. Тот
факт, что
i
B
|
A
почти всегда отрицательна кроме случая
q
=
1
2
, как
раз отражает то, что подсистема
А
почти всегда квантовая. При мак-
симальной смешанности, достигаемой при
q
=
1
2
, подсистема не запу-
тана
(
C
= 0)
, но классически максимально коррелирована (
i
B
|
A
= 0)
при любом
a
2
.
На рис. 14 показанызависимости
с
2
и
γ
от
q
и
a
2
. Положительная
величина
с
2
показывает, что почти при всех
q
и
a
2
А
есть причина,
В
—
следствие. Причинность исчезает (
c
2
=
∞
)
только при
q
= 0
или 1
(чистое состояние) и
a
2
=
1
2
(симметричное состояние). Направление
причинной связи
А
→
В
проясняет вывод [6] о большей хрупкости к
декогеренции подсистемы
В
. Сток квантовой информации, т.е. пере-
ход запутанности к окружению, происходит преимущественно в более
диссипативной подсистеме
В
.
34
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4