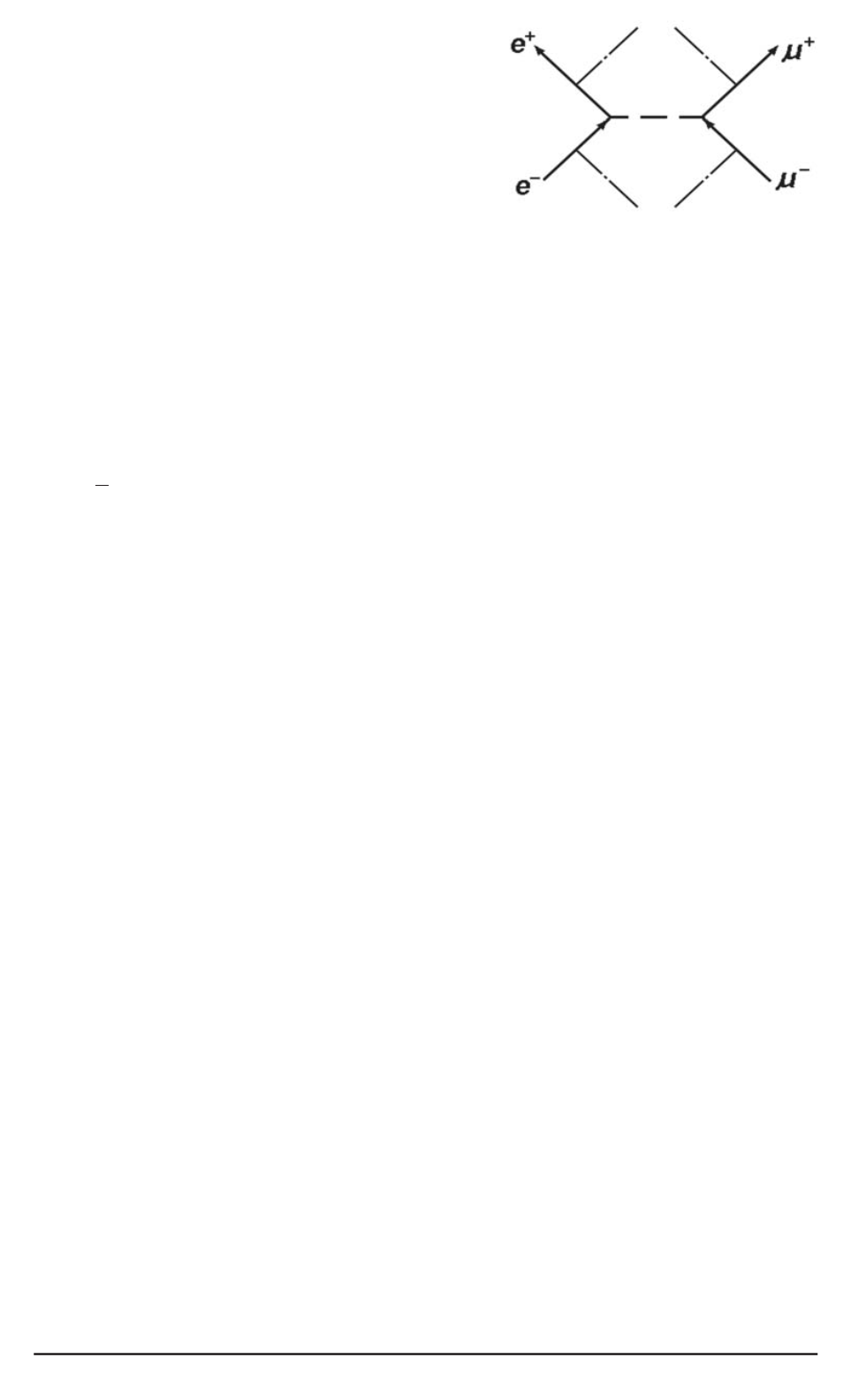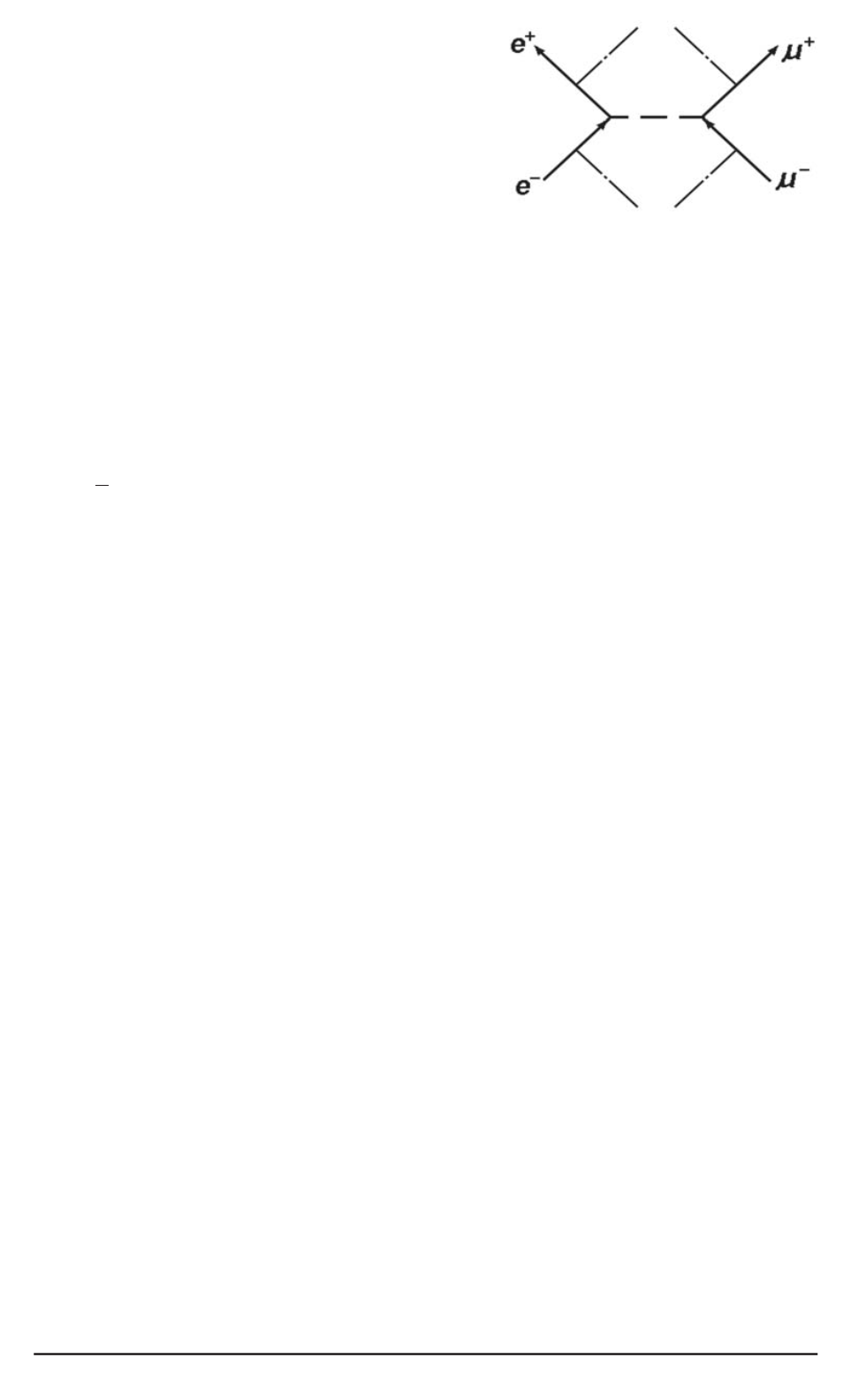
Рис. 3. Диаграмма Фейнмана
для процесса рождения фото-
нов мнимого электромагнитно-
го поля
пионов на нуклонах. При этом возможно
два варианта для доли каонов или пио-
нов с мнимым спином: либо 7,8% (если
спиновая инверсия происходит вирту-
ально), либо 0,61% (если спиновая ин-
версия происходит реально). Эти оценки
взяты из п. 6 настоящей работы.
Третьим возможным направлением
являются эксперименты по поиску фо-
тонов мнимого электромагнитного по-
ля, которое, видимо, должно существо-
вать и источником которого должен являться мнимый магнитный мо-
мент, связанный с мнимым спиновым моментом импульса. Использу-
ем обычное определение для плотности энергии электромагнитного
поля
1
2
(
ε
0
εE
2
+
μ
0
μH
2
)
, но поскольку для мнимого поля векторы
Е
и
Н
— мнимые, энергия становится отрицательной. Соответственно, и
фотоны такого поля должны иметь отрицательную энергию. Именно
этот факт и можно было бы использовать для обнаружения рождения
фотонов мнимого поля.
Наиболее интересным, видимо, был бы эксперимент по электрон-
позитронной аннигиляции с рождением мюон-антимюонной пары и
фотонов мнимого электромагнитного поля. Диаграмма Фейнмана низ-
шего порядка для такого процесса представлена на рис. 3, где пунктир-
ная линия означает виртуальный вещественный фотон, а штриховая —
реальный мнимый фотон. Рождение мюон-антимюонной пары (а не
просто электрон-позитронное рассеяние) необходимо для того, что-
бы получить точную информацию, что взаимодействие действительно
произошло. С учетом мюон-антимюонного рождения энергия элек-
тронного (позитронного) пучка должна быть порядка 0,5 ГэВ и выше.
Как видно на рис. 3, на диаграмме Фейнмана низшего порядка должно
родиться сразу четыре мнимых фотона. Это связано с двумя законами
сохранения: мнимого момента (для того чтобы ему удовлетворить, чи-
сло рождающихся мнимых фотонов должно быть четным) и спиновой
четности. Так как спиновая четность обычных частиц — единица, а
спиновая четность мнимых фотонов
i
, то для ее сохранения нужно
рождение четырех мнимых фотонов, так как
i
4
= 1
.
Вероятность рождения мнимых фотонов рассчитаем, основываясь
на двух предположениях: а) константа связи та же, что и для обычного
электромагнитного взаимодействия; б) вероятность рождения частицы
(фотона) с мнимым спином такова же, как и вероятность спиновой
инверсии, рассчитанной в п. 6 настоящей работы. Тогда вероятность
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4
83