С учетом всего сказанного для проекции на ось
z
в декартовой си-
стеме координат получаются следующие восемь вариантов оператора:
Π
z
=
±
z
c
∂
∂t
+
ct
∂
∂z
±
i x
∂
∂y
−
y
∂
∂x
Π
z
=
±
i
z
c
∂
∂t
+
ct
∂
∂z
±
x
∂
∂y
−
y
∂
∂x
.
(3)
Аналогичные формулы получаются для проекций на оси
x
и
y
.
Непосредственный вывод показывает, что все операторы проекций
(на оси
x
,
y, z
) коммутируют с оператором квадрата спина (1), что
свидетельствует об одновременной измеримости спинового момента
и одной (любой) изего проекций.
Для дальнейшего операторы проекций (3) удобно записать в виде
Π
Nz
=
α
N
z
c
∂
∂t
+
ct
∂
∂z
+
β
N
x
∂
∂y
−
y
∂
∂x
.
(4)
Аналогичные формулы получаются для проекций на оси
x
и
y
.
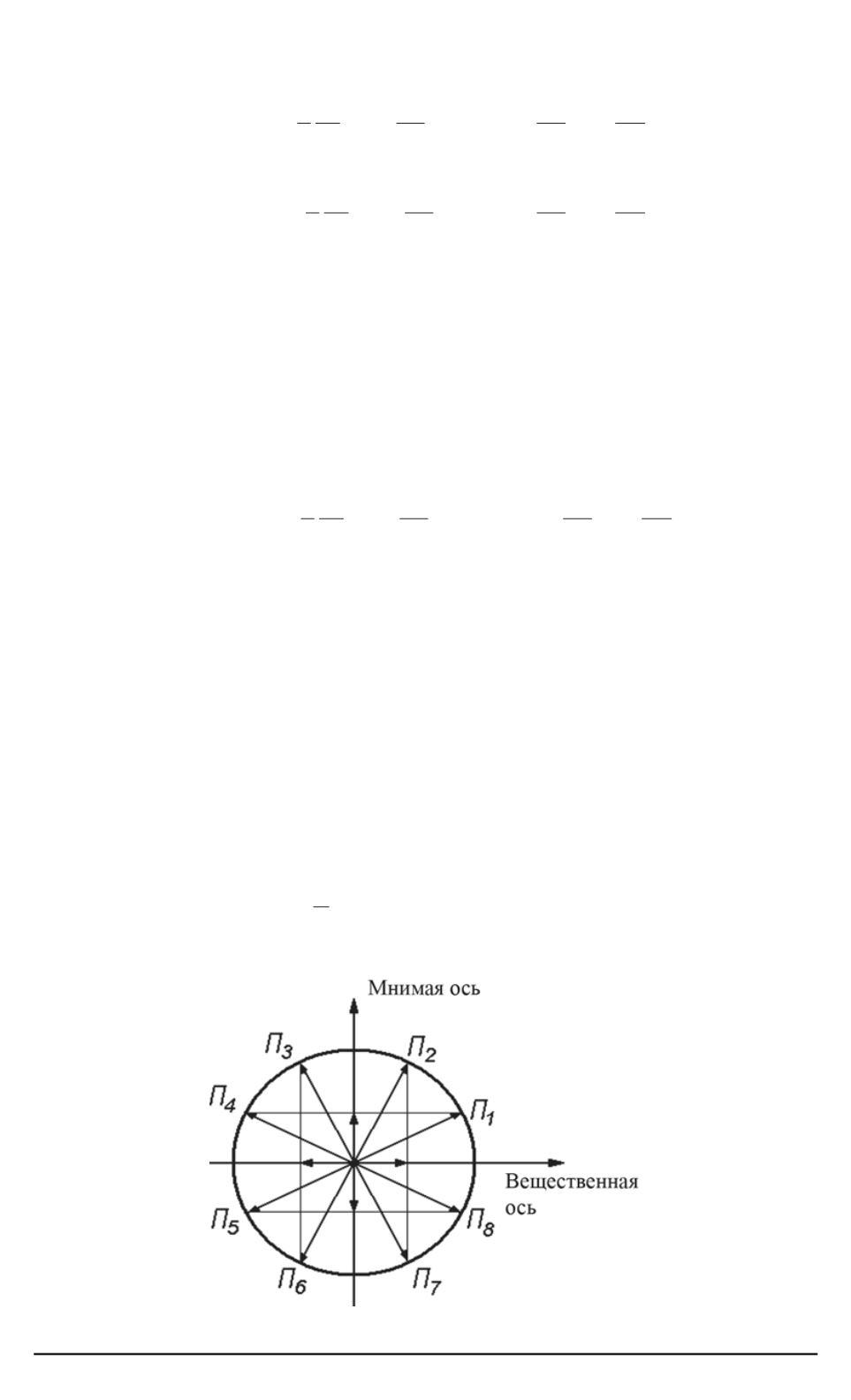
Если символически изобразить операторы, как это сделано на рис. 1,
и пронумеровать их против часовой стрелки, то коэффициенты
α
N
и
β
N
принимают значения, указанные в таблице.
Как будет показано ниже, четыре оператора (
Π
2
,
Π
3
,
Π
6
,
Π
7
) дают
вещественную проекцию спина, а другие четыре оператора (
Π
1
,
Π
4
,
Π
5
,
Π
8
) — мнимую проекцию. Изтаблицы видно, что одна четвер-
ка операторов преобразуется в другую умножением на
i
, а именно
i
Π
N
= Π
N
+2
(с циклической перестановкой). На рис. 1 это соответ-
ствует повороту на угол
π
2
.
Рис. 1. Символическое изображение операторов проекции спина
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2010. № 4


