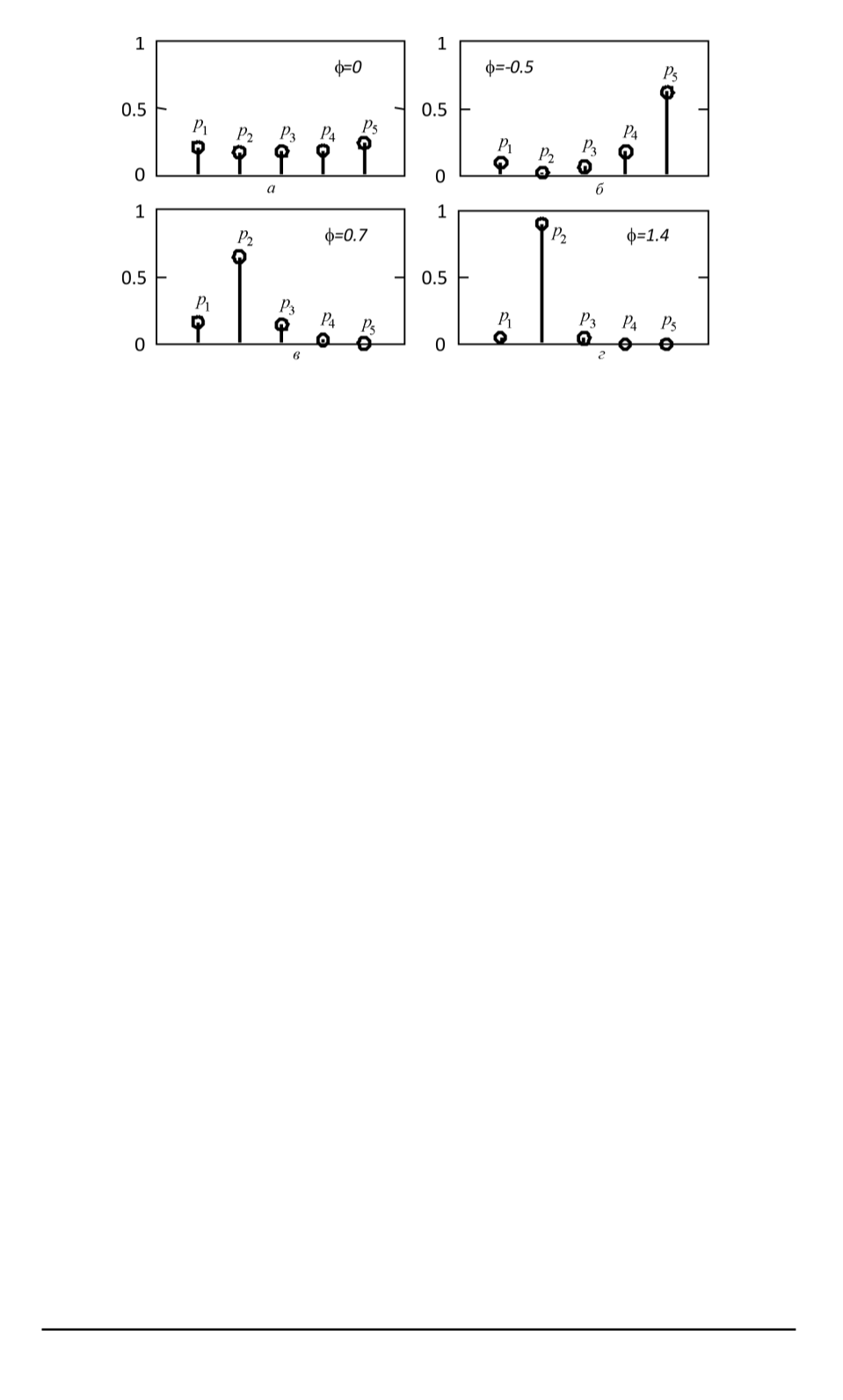
Рис. 8. Распределения вероятностей на элементах мультиаттрактора системы
(1) при различных значениях
φ
, соответствующие зависимостям рис. 3:
а
—
φ
= 0
;
б
—
φ
=
−
0
,
5
(
ν
≈ −
0
,
23
);
в
—
φ
= 0
,
7
(
ν
≈
0
,
33
);
г
—
φ
= 1
,
4
(
ν
≈
0
,
65
)
Итак, в самых различных вариантах составных мультиаттракто-
ров — от простейших, содержащих только два локальных аттрактора,
до значительно более сложных, с большим числом элементов, суще-
ствует зависимость вероятностей локализации движения на локальных
аттракторах от положения границ содержащих их ячеек фазового про-
странства.
При этом уже в простейшем случае одинакового по модулю смеще-
ния положения границ между соседними локальными аттракторами,
можно получать значительное разнообразие распределений вероятно-
стей на множестве локальных аттракторов, в частности: переходить от
распределения, близкого к равномерному (рис. 8,
а
и 9,
а
), к локализа-
ции движения преимущественно на одном из локальных аттракторов
(рис. 8,
б–г
и 9,
б, в
), а также реализовать некоторые более сложные
ситуации (рис. 9,
г
).
Очевидно, что в более общем случае произвольных по величине
и направлению смещениях границ каждой фазовой ячейки возможна
реализация практически любого априорного распределения вероятно-
стей на множестве локальных аттракторов. Причем для этого достаточ-
но модифицировать только операторы редупликации без какого-либо
специального вмешательства в динамику движения на хаотических
аттракторах, образующих мультиаттрактор.
Соответствие между параметрами реплицирующих операторов,
определяющими величину смещения границ фазовых ячеек, и распре-
делениями вероятностей на элементах составного мультиаттрактора
является детерминированным и задает закон управления. Однако
объектом управления являются не элементы самого движения, а веро-
ятности их осуществления. Состояние такой динамической системы,
независимо от управляющего воздействия, может самопроизвольно
70
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1


