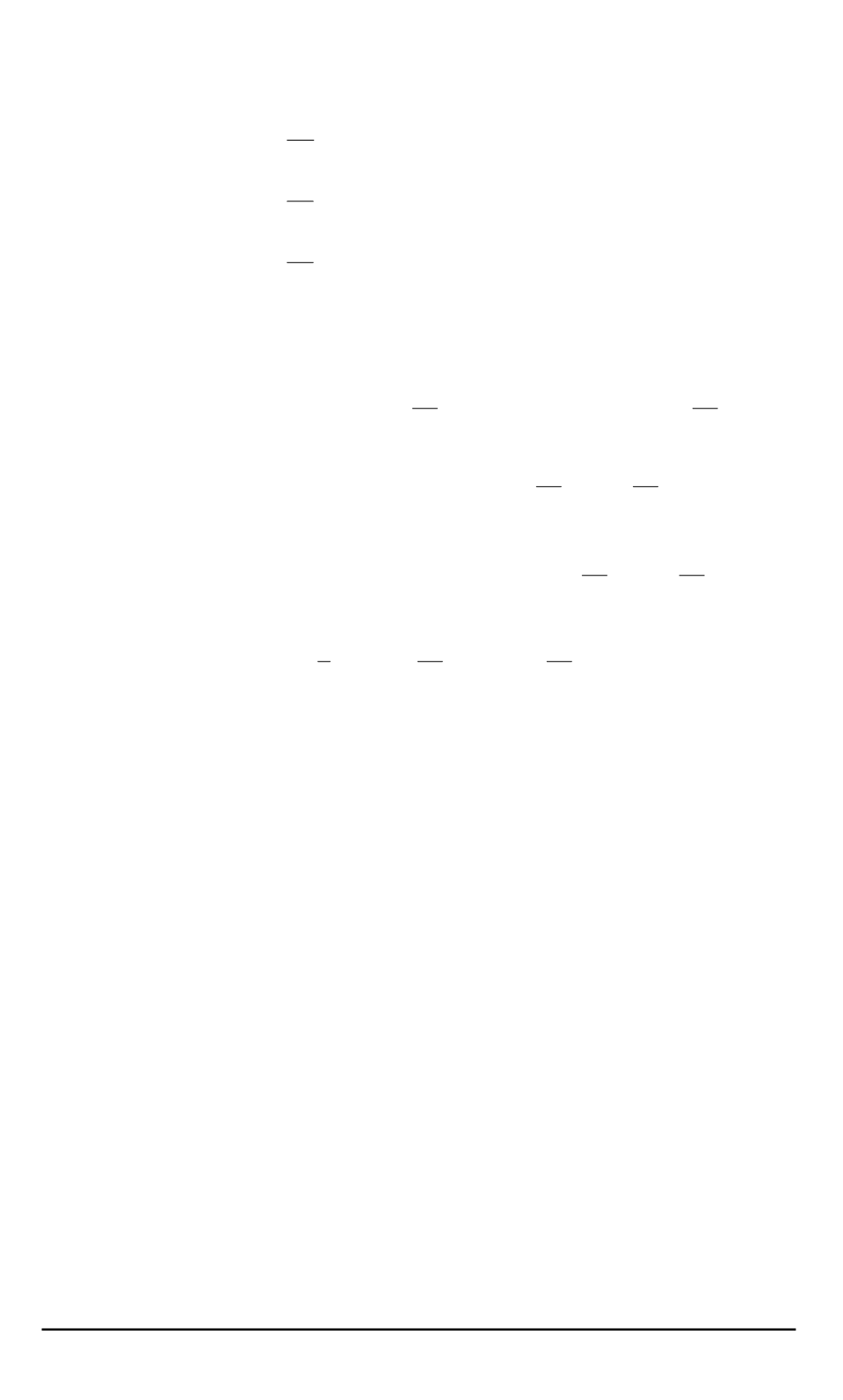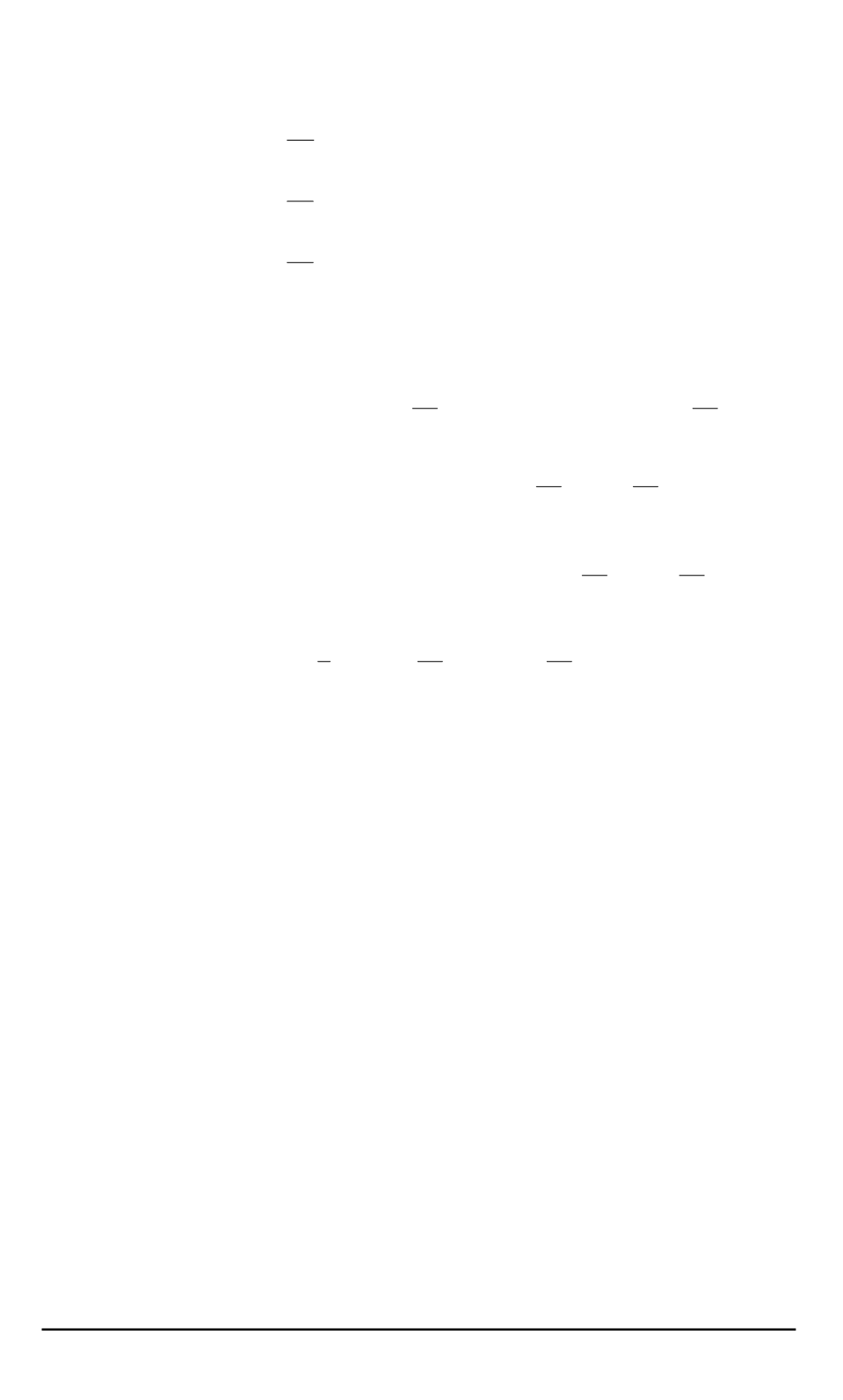
с системы, имеющей мультиаттрактор, объединяющий исходный ат-
трактор Лоренца и его копии, упорядоченные по координате
x
[5]:
dx
dτ
=
A
(
y
−
H
1
(
x
)) ;
dy
dτ
=
H
1
(
x
) (
B
−
z
)
−
y
;
dz
dτ
=
H
1
(
x
)
y
−
Cz,
(1)
где
H
k
(
ξ
k
) =
ξ
k
+
+ (
d
k
+ 1)
P ξ
k
+
s
k
+
h
k
+
h
k
d
k
+
P ξ
k
+
s
k
−
h
k
−
h
k
d
k
−
−
M
k
X
j
=0
P ξ
k
+
s
k
−
(2
j
−
1)
h
k
+
h
k
d
k
+
h
k
d
k
−
−
N
k
X
j
=0
P ξ
k
+
s
k
+ (2
j
−
1)
h
k
+
h
k
d
k
−
h
k
d
k
,
(2)
P
(
ξ
k
) =
1
2
ξ
k
+
h
k
d
k
−
ξ
k
−
h
k
d
k
,
— реплицирующий оператор, отвечающий за образование копий ат-
трактора исходной динамической системы, упорядоченных по коор-
динате
ξ
k
(для системы (1)
k
= 1
,
ξ
1
=
x
), и их объединение в единый
мультиаттрактор [6]. Число локальных аттракторов в составе муль-
тиаттрактора системы (1), (2) равно
1 +
M
+
N
. Каждый из них на-
ходится внутри собственной области фазового постранства (фазовой
ячейки) протяженностью
2
h
по координате
x
. Константа
s
учитывает
асимметрию локальных аттракторов относительно центра своей ячей-
ки. Коэффициент
d
определяет расстояние между соседними ячейками
(равное
2
h/d
) [1, 6].
Возьмем для начала простейший мультиаттрактор, содержащий ис-
ходный аттрактор и одну его копию (рис. 1), приняв
А
= 10
,
В
= 30
,
С
= 2
,
6
и
M
1
= 1
,
N
1
= 0
,
h
1
= 17
,
s
1
= 0
,
d
1
= 10
. Так как хаоти-
ческий аттрактор Лоренца симметричен по координате
x
, он и его
копия пересекаются с границами своих фазовых ячеек строго симме-
трично (рис. 1,
а, б
). То есть границы ячеек отсекают равные доли
на обращенных друг к другу сторонах обоих аттракторов. При этом
переходы фазовых траекторий между аттракторами равновероятны и
изображающая точка находится в обеих областях притяжения в сред-
нем одинаковое время (рис. 1,
в
).
62
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1