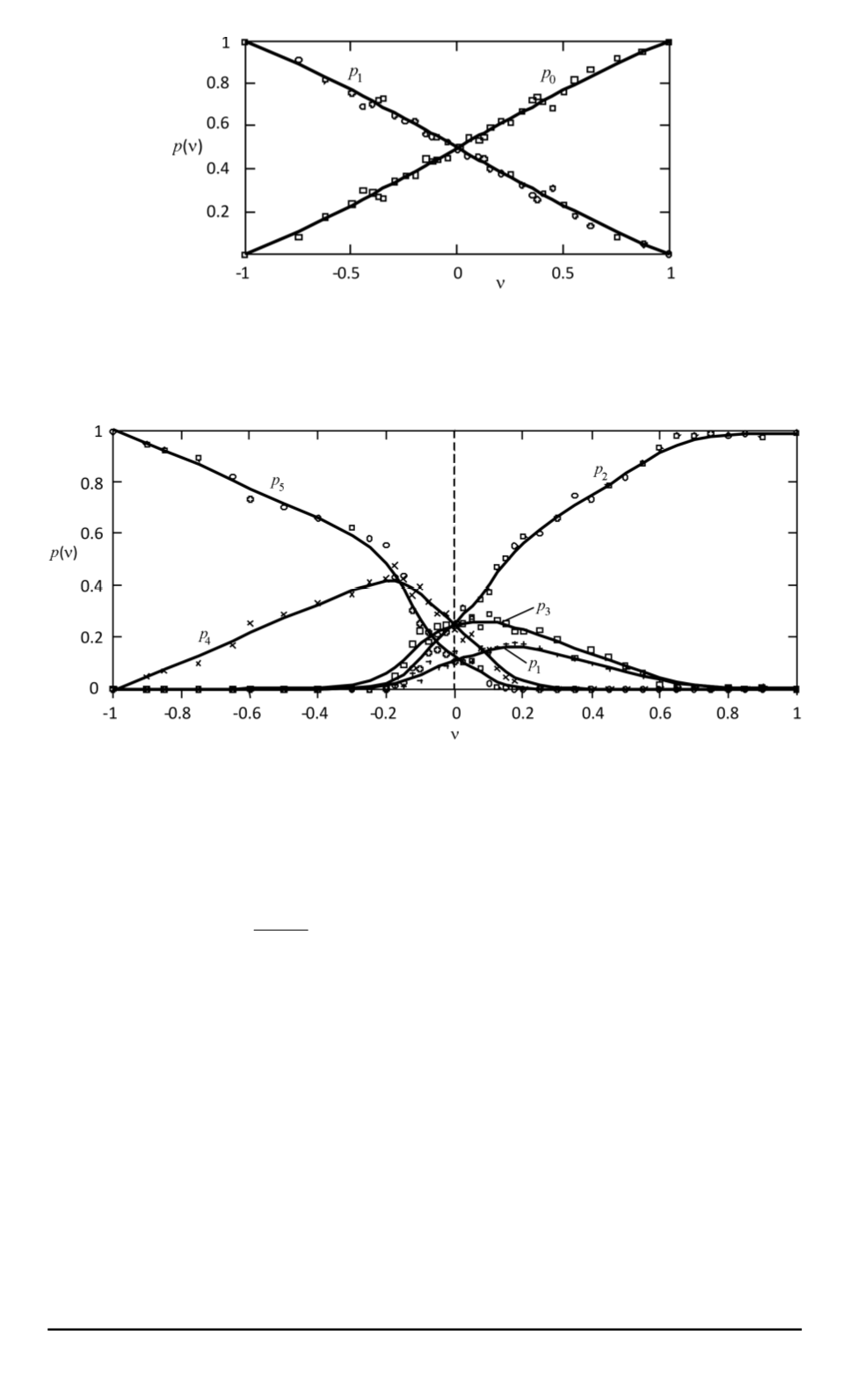
Рис. 6. Зависимость распределения вероятностей на локальных аттракторах
двухэлементного мультиаттрактора системы (9) от величины смещения границ
ячеек относительно симметричного положения:
◦
, — числовые данные; линии — аппроксимирующие функции (4)
Рис. 7. Зависимость распределения вероятностей на элементах мультиаттракто-
ра системы (9), состоящего из пяти аттракторов Чуа, от величины показанного
на рис. 4 смещения границ ячеек относительно симметричного положения:
◦
, ,
+
,
×
— числовые данные; линии — аппроксимирующие сглаженные функции
где
f
(
x
) =
bx
+
a
−
b
2
(
|
x
+ 1
| − |
x
−
1
|
)
, с параметрами
А
= 9
,
4
,
В
= 15
,
a
=
−
2
,
6
,
b
=
−
0
,
4
,
h
= 2
,
14
,
s
= 0
, в которой элемен-
тами мультиаттрактора являются аттракторы Чуа, упорядоченные по
координате
y
[9]. Интересно, что показанная на рис. 6 зависимость
распределения вероятностей для двухэлементного мультиаттрактора
(
M
2
= 1
,
N
2
= 0
) системы (8) также может быть аппроксимирована
выражениями (4) при
α
= 1
,
1
. Зависимости на рис. 7 для пятиэлемент-
ного мультиаттрактора (
M
2
= 2
,
N
2
= 2
) системы (8) соответствуют
такому же варианту смещения границ фазовых ячеек относительно
симметричного положения, что и зависимости на рис. 3. Сравнение
рис. 3 и 7 показывает, что, несмотря на существенные различия в ди-
намике систем (1) и (9), эти зависимости качественно подобны.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1
69


