по направлению
у
+
μ
х
в динамической системе [1]
dx
dτ
=
A
[
H
2
(
y
+
μx
)
−
(1 +
μ
)
x
] ;
dy
dτ
=
x
[
B
−
z
+
μ
]
−
H
2
(
y
+
μx
) ;
dz
dτ
= [
H
2
(
y
+
μx
)
−
μx
]
x
−
Cz
(6)
(например, при
А
= 10
,
В
= 30
,
С
= 2
,
6
,
M
2
= 1
,
N
2
= 0
,
h
2
= 21
,
s
2
= 0
,
d
2
= 10
,
μ
=
−
0
,
2
)
или по направлению
z
в системе
dx
dτ
=
A
(
y
−
x
) ;
dy
dτ
=
x
(
B
−
H
3
(
z
))
−
y
;
dz
dτ
=
xy
−
CH
3
(
z
)
(7)
(например, при
А
= 10
,
В
= 30
,
С
= 2
,
6
,
M
3
= 1
,
N
3
= 0
,
h
3
= 19
,
1
,
s
3
= 27
,
3
) [1].
Для простейших мультиаттракторов на основе аттрактора Лоренца
распределения вероятностей инвариантны к изменению
φ
max
, причем
коэффициент
α
сохраняет значение 2.
В случае большего, чем два, числа локальных аттракторов в со-
ставе мультиаттрактора системы (1), (3) также наблюдается перерас-
пределение вероятностей в пользу наименее ”усеченных” локальных
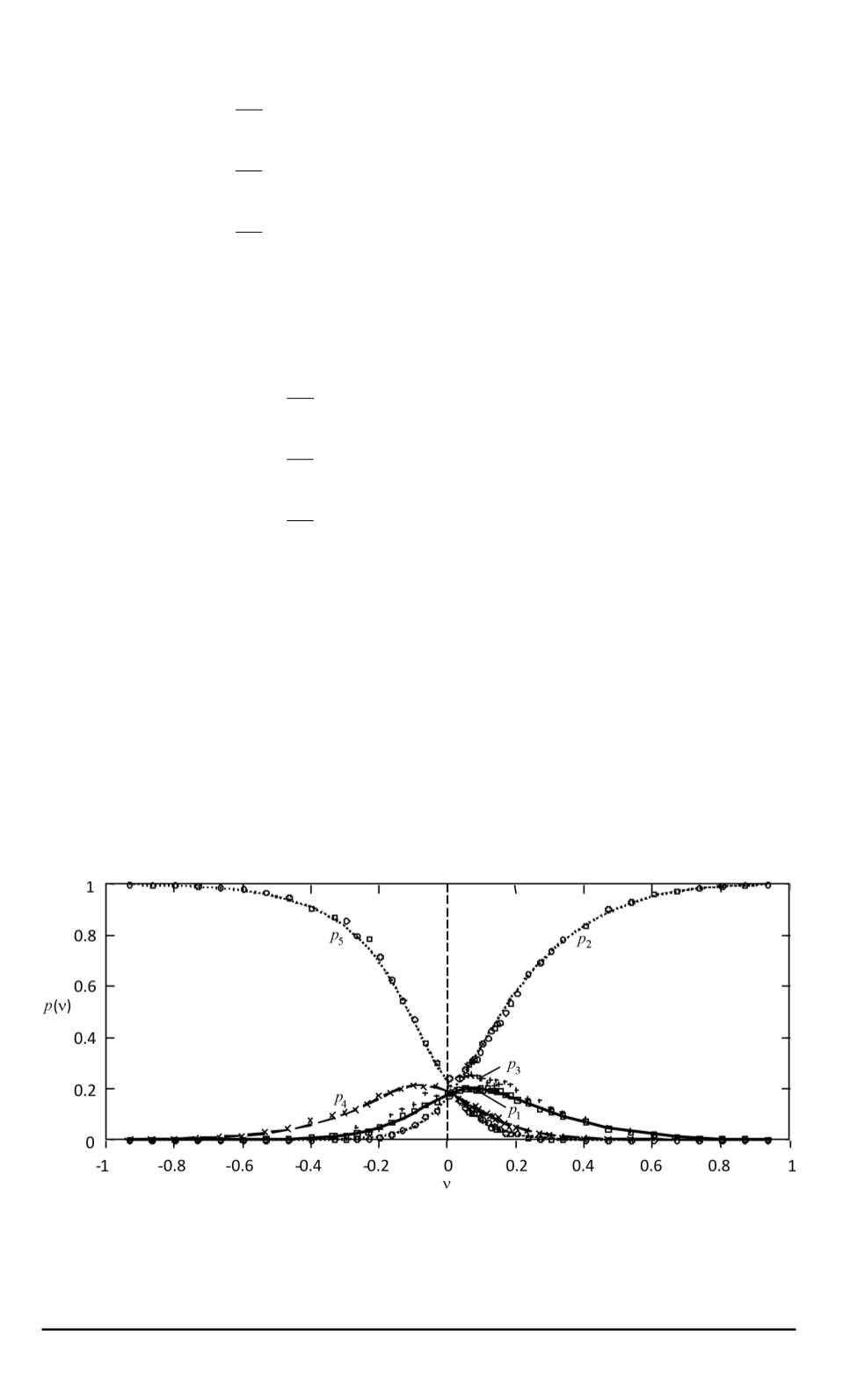
аттракторов. На рис. 3 приведена зависимость распределения веро-
ятностей пребывания фазовой точки на элементах мультиаттрактора
Рис. 3. Зависимость распределения вероятностей на элементах мультиаттракто-
ра системы (1), состоящего из пяти аттракторов Лоренца, от величины смеще-
ния границ ячеек фазового пространства, содержащих локальные аттракторы,
относительно симметричного положения:
◦
, ,
+
,
×
— числовые данные; линии — аппроксимирующие сглаженные функции
66
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 1


