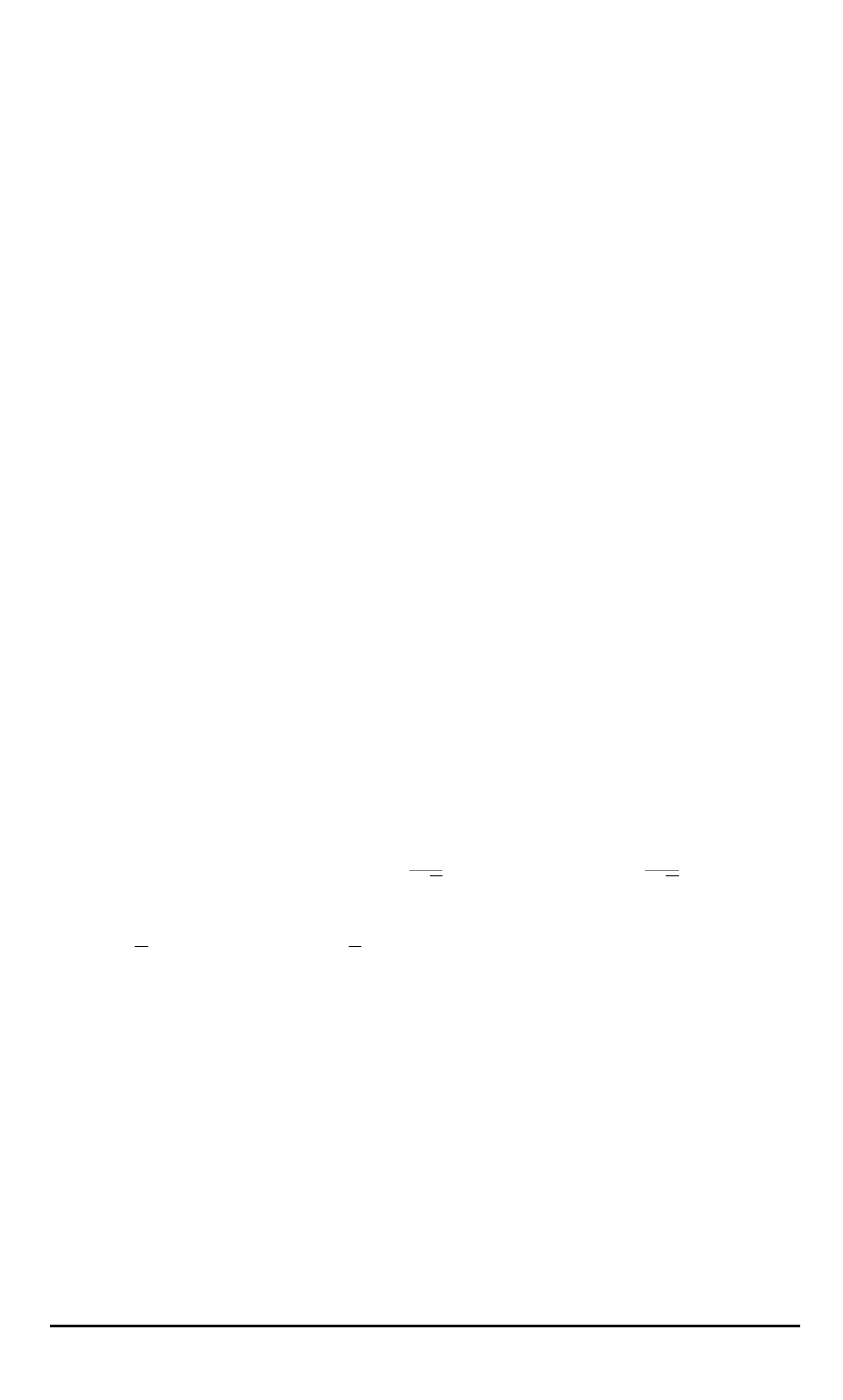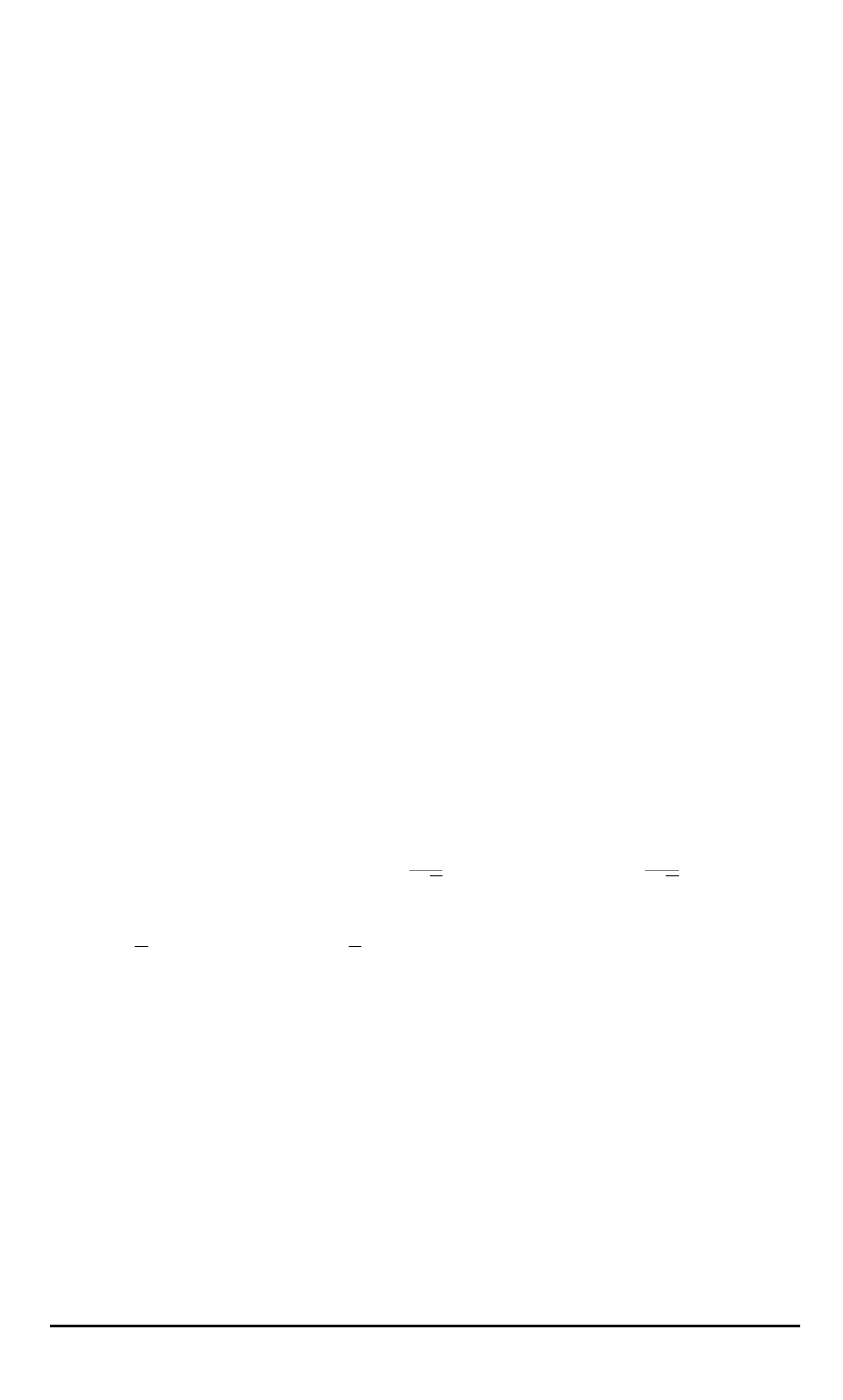
непрерывных процессах деформирования, т.е. при отсутствии разру-
шения. Однако сам процесс проникания ударников в преграду как раз
и состоит из стадий зарождения трещин, их распространения и обра-
зования отверстия в преграде. При численных расчетах этот процесс
моделируется следующим образом.
Этап зарождения трещин.
В процессе непрерывного деформи-
рования в каждой расчетной точке ударника и мишени проверяется
условиe отсутствия разрушения
π
α
<
1
, где
π
α
— параметры повре-
ждаемости материала, представляющие собой функции инвариантов
тензора истинных напряжений Коши (силовой критерий):
π
α
=
π
α
(
Y
β
(
T
ij
))
.
(36)
Инварианты выбираются в соответствии с группой симметрии рассма-
триваемого материала (изотропные, трансверсально-изотропные или
ортотропные). Критерий прочности преграды в этом случае оказыва-
ется подобным критериям пластичности, но только пределы текуче-
сти в них заменяются на соответствующие пределы прочности. Для
трансверсально-изотропных материалов рассмотрим модель, содержа-
щую два параметра повреждаемости:
π
1
= (
Y
+
1
/σ
1
T
)
2
+ (
Y
1
/σ
1
T
)
2
+ (
Y
4
/σ
4
S
)
2
;
π
2
= (
Y
+
2
/σ
2
T
)
2
+ (
Y
2
/σ
2
C
)
2
+ (
Y
3
/σ
3
S
)
2
,
(37)
где
σ
γT
,
σ
γC
σ
γS
— пределы прочности на растяжение, сжатие и сдвиг
в соответствующем направлении, а инварианты тензора напряжений
определяются следующим образом:
Y
1
=
T
zz
;
Y
2
=
T
rr
+
T
ϕϕ
;
Y
3
=
1
√
2
|
T
rr
−
T
ϕϕ
|
;
Y
4
=
1
√
2
|
T
rz
|
;
Y
+
1
=
1
2
(
Y
1
+
|
Y
1
|
);
Y
−
1
=
1
2
(
|
Y
1
| −
Y
1
);
Y
+
2
=
1
2
(
Y
2
+
|
Y
2
|
);
Y
−
2
=
1
2
(
|
Y
2
| −
Y
2
)
.
(38)
В соответствии с этой моделью существуют два независимых па-
раметра повреждаемости, один из которых описывает повреждения в
поперечном направлении и при межслойных сдвигах, а другой — в про-
дольном направлении и при продольных сдвигах. Эта модель хорошо
описывает эффекты разрушения продольно-поперечно армированных
материалов.
Для изотропных сред рассматривается модель с одним параметром
повреждаемости, для которого выбрано следующее выражение:
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4
109