Вычисляем матрицу Якоби
Q
=
∂s
∂z
∂τ
∂z
∂s
∂r
∂τ
∂r
=
∂z
∂s
∂r
∂s
∂z
∂τ
∂r
∂τ
−
1
.
(30)
для перехода от координат
(
s, τ
)
к координатам
(
z, r
)
.
В данной работе функции (29) аппроксимировали кубическими
сплайнами, заданными опорными точками. В каждом из криволиней-
ных четырехугольников
V
i
введена локальная разностная сетка, затем
отдельные сетки для каждого четырехугольника объединены в единую
разностную сетку, охватывающую всю область
V
.
Отличительная особенность алгоритма построения разностной
сетки состоит в том, что узлы единой разностной сетки пронуме-
рованы единым списком (сетка при этом описывается ленточным
образом) и их характеристики (координаты в системах
(
z, r
)
и
(
s, τ
)
,
элементы обратной матрицы Якоби, номера соседних узлов) предста-
влены единым списком. Кроме того, в сеточных массивах помещена
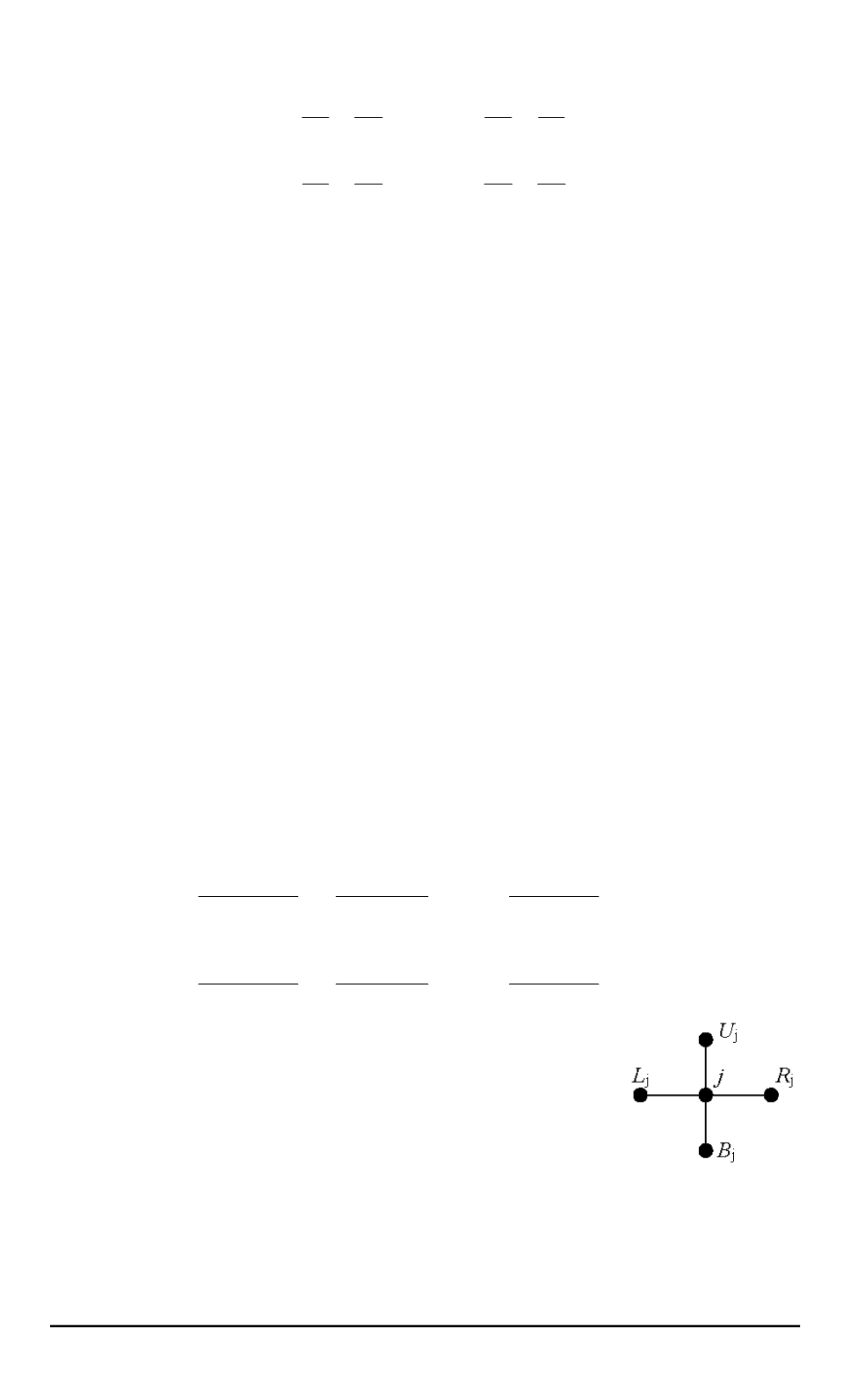
информация о номерах соседних четырех узлов, которым присвое-
ны индексы
L
j
, R
j
, B
j
, U
j
, обозначающие номера соседей
j
-го узла
слева, справа, снизу и сверху соответственно (рис. 3). Координаты
узла сетки при таком подходе обозначаются как (
S
j
, T
j
)
, разностные
аппроксимации функции
f
(
s, τ
)
— как
f
j
=
f
(
S
j
, T
j
)
, а разностные
аппроксимации производных принимают следующий вид (например,
правая разность):
∂f
(
r
j
, z
j
)
∂r
≈
f
R
j
−
f
j
S
R
j
−
S
j
Q
11
j
+
f
U
j
−
f
j
T
U
j
−
T
j
Q
12
j
;
∂f
(
r
j
, z
j
)
∂z
≈
f
R
j
−
f
j
S
R
j
−
S
j
Q
21
j
+
f
U
j
−
f
j
T
U
j
−
T
j
Q
22
j
.
(31)
Рис. 3. Узел раз-
ностной сетки с
четырьмя сосед-
ними узлами в
ЛАС
Такую разностную аппрокимацию функций и
производных использовали для построения раз-
ностной схемы системы уравнений (23). Был приме-
нен один из наиболее экономичных по затратам ма-
шинного времени конечно-разностный метод реше-
ния системы (23) — метод типа Мак-Кормака [13],
состоящий из четырех этапов; во введенных обо-
значениях он принимает следующий вид.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 4
107


