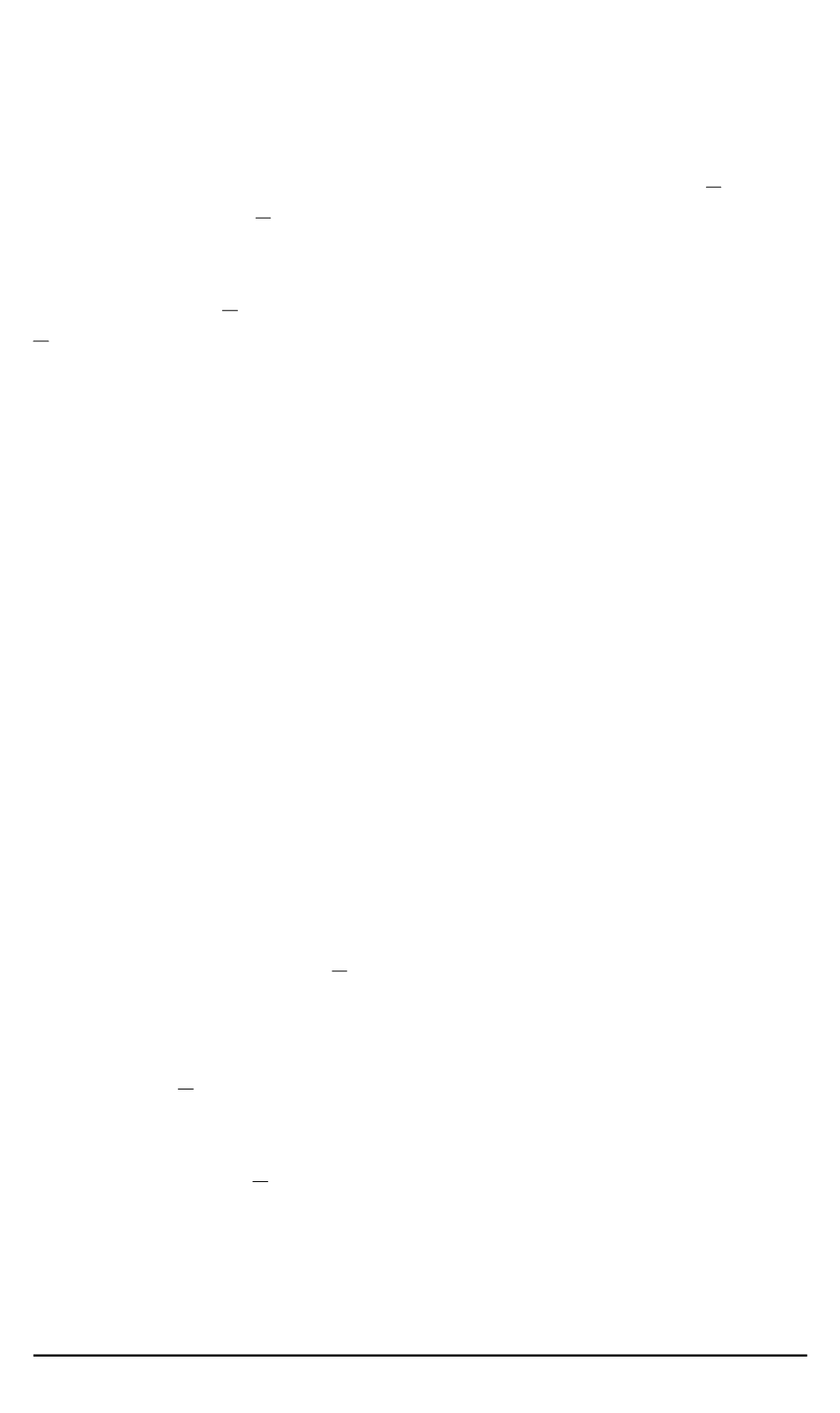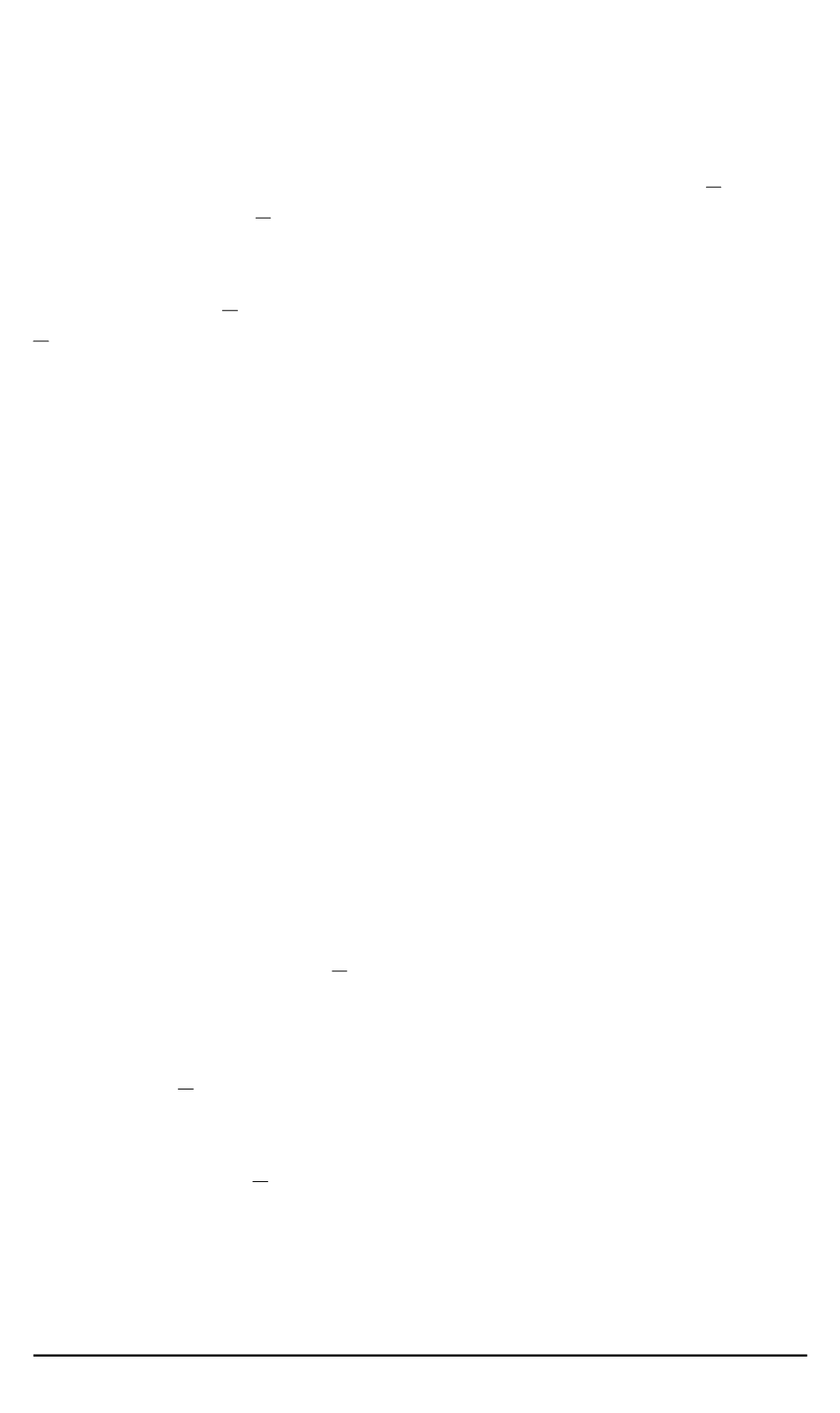
где максимум берется по всем значениям вектора параметров
λ
при-
надлежащим
γ
-доверительному множеству
H
(
d
)
в пространстве пара-
метров
λ
[1, 2]. Наиболее простым вариантом данного подхода явля-
ется метод, основанный непосредственно на частных доверительных
границах для параметра надежности отдельных режимов
λ
j
. В этом
случае множество
H
(
d
)
задается неравенствами
0
6
λ
j
6
λ
j
(
d
j
, γ
0
)
(
j
= 1
, ..., m
), где
λ
j
(
d
j
, γ
0
)
— стандартная верхняя доверительная
граница с коэффициентом доверия
γ
0
, вычисленная по результатам
испытаний
d
j
в
j
-м режиме. При этом результирующий коэффици-
ент доверия для
f
определяется как
γ
=
γ
m
0
. Доверительная граница
f
для показателя надежности системы вычисляется при этом путем
простой подстановки частных доверительных границ для отдельных
параметров
λ
j
в функцию
f
(
λ, t
)
. В задаче оценки надежности для
случая переменного режима данный подход (“метод прямоугольника”
или сокращенно МП) использовался ранее в работах [3], [4] и др.
Аналогичный подход использовался также в ряде работ, связанных с
оценкой надежности сложных систем по результатам испытаний их
отдельных компонентов: [1], [2], [7–16] и др. Недостатком этого ме-
тода является снижение эффективности при увеличении размерности
задачи (количества различных режимов)
m
.
Отметим, что в рассматриваемой здесь постановке данный метод
может быть значительно улучшен за счет указанной выше дополни-
тельной априорной информации о монотонном возрастании интен-
сивности отказов системы
λ
(
U
)
при возрастании внешней нагруз-
ки. Исходя из этого, значения параметров интенсивности отказов в
различных режимах
λ
j
можно считать упорядоченными. Для опреде-
ленности рассматривается случай, когда это упорядочение имеет вид
λ
1
6
λ
2
6
. . .
6
λ
m
. С учетом указанных неравенств искомая довери-
тельная граница далее вычисляется в соответствии с (1), где максимум
берется при ограничениях
0
6
λ
j
6
λ
j
(
d
j
, γ
0
)
, j
= 1
, . . . , m
;
(2)
λ
1
6
λ
2
6
. . .
6
λ
m
.
(3)
Нетрудно видеть, что получаемая таким образом верхняя доверитель-
ная граница
f
будет заведомо лучше (меньше) по сравнению с ука-
занным выше обычным МП. Данный подход назовем “модифициро-
ванным методом прямоугольника” (ММП). В отличие от обычного
МП, для которого
f
легко находится аналитически, для ММП эта
величина в общем случае не вычисляется аналитически, но может
быть достаточно просто найдена с помощью численного алгоритма
на основе следующей далее теоремы 1. Пусть
λ
0
= (
λ
0
1
, λ
0
2
, . . . , λ
0
m
)
—
точка, в которой достигается максимум (1) для исходной задачи МП.
62
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 3