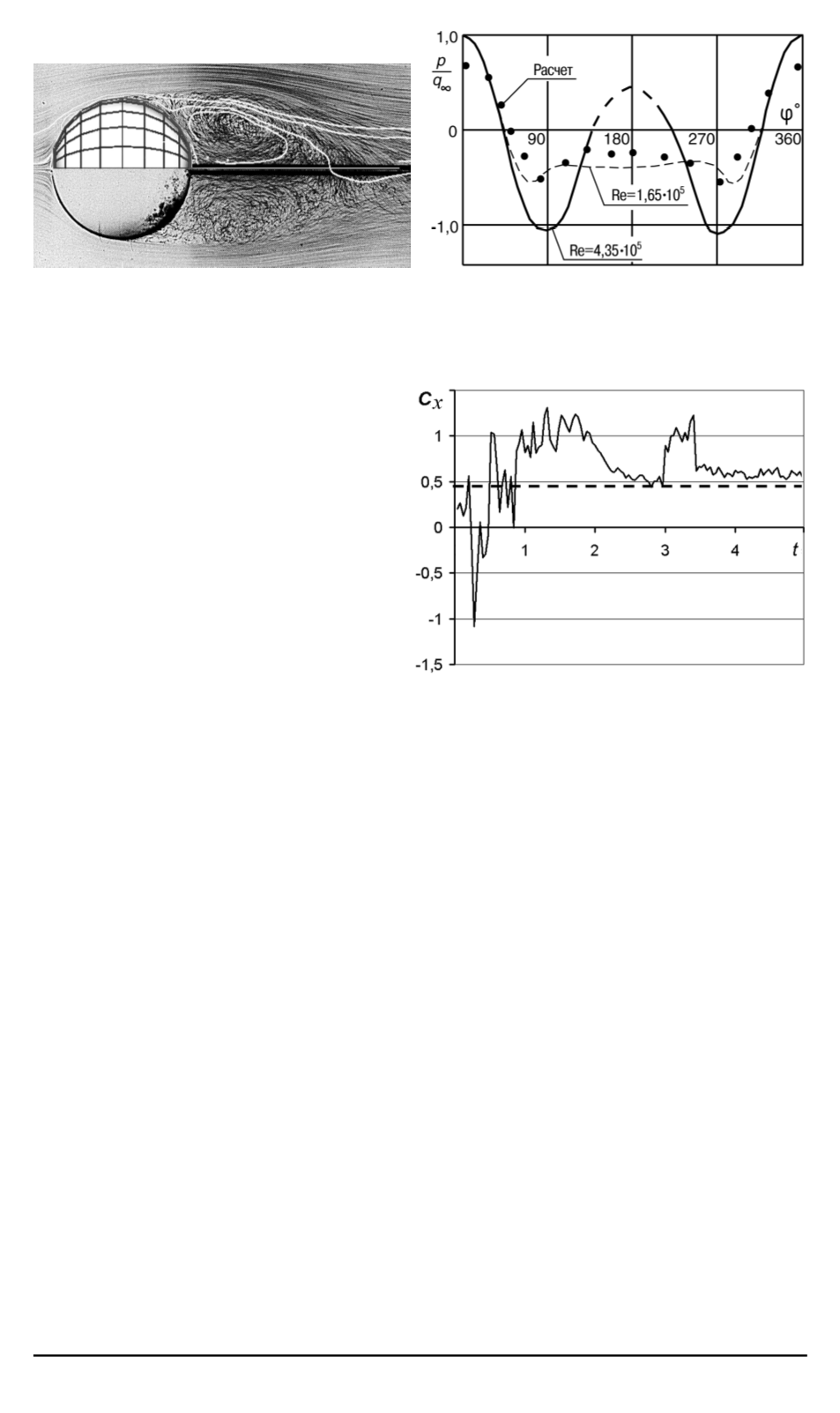
Рис. 3. Вычисленные линии тока в
сравнении с экспериментом [12]
Рис. 4. Распределение давления в срав-
нении с экспериментом [13]
Рис. 5. Вычисленные значения коэффи-
циента сопротивления в сравнении с
результатами эксперимента (штриховая
линия) [13]
На pис. 4 показано распре-
деление давления на поверхно-
сти для докритического и за-
критического течения [13]. Бы-
ли построены 60 эпюр
p
(
ϕ
)
,
вычисленных на каждом ша-
ге по времени в интервале
t
2
[4
,
6; 6
,
8]
. Для модели-
рования эффекта демпфирова-
ния пульсаций давления измери-
тельной аппаратурой в числен-
ном эксперименте давление для
каждой точки эпюры
p
(
ϕ
)
бы-
ло взято средним на интервале
t
2
[4
,
6; 6
,
8]
. Эти средние значения указаны на рис. 4 точками.
На рис. 5 дан график изменения во времени осевой составляющей
силы сопротивления в сравнении с результатом для Re
= 15000
из ра-
боты [13]. Среднее значение, найденное по результатам вычислений,
C
x
= 0
,
57
. Разница с экспериментальным значением
C
x
э
= 0
,
49
соста-
вляет 16%.
Расчет, в котором было выполнено 170 полных циклов вычисли-
тельного конвейера, занял на персональном компьютере с процессо-
ром Pentium IV (2,6 ГГц) 16 часов. Для решения аналогичной неста-
ционарной задачи методом конечных объемов потребовалось на том
же компьютере 120 часов расчета.
Выводы.
Построена модификация метода вихревых частиц для
численного моделирования пространственных нестационарных тече-
ний идеальной жидкости с использованием вортонных рамок на теле
для удовлетворения граничного условия непротекания и вычисления
нестационарных нагрузок.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 2
111


