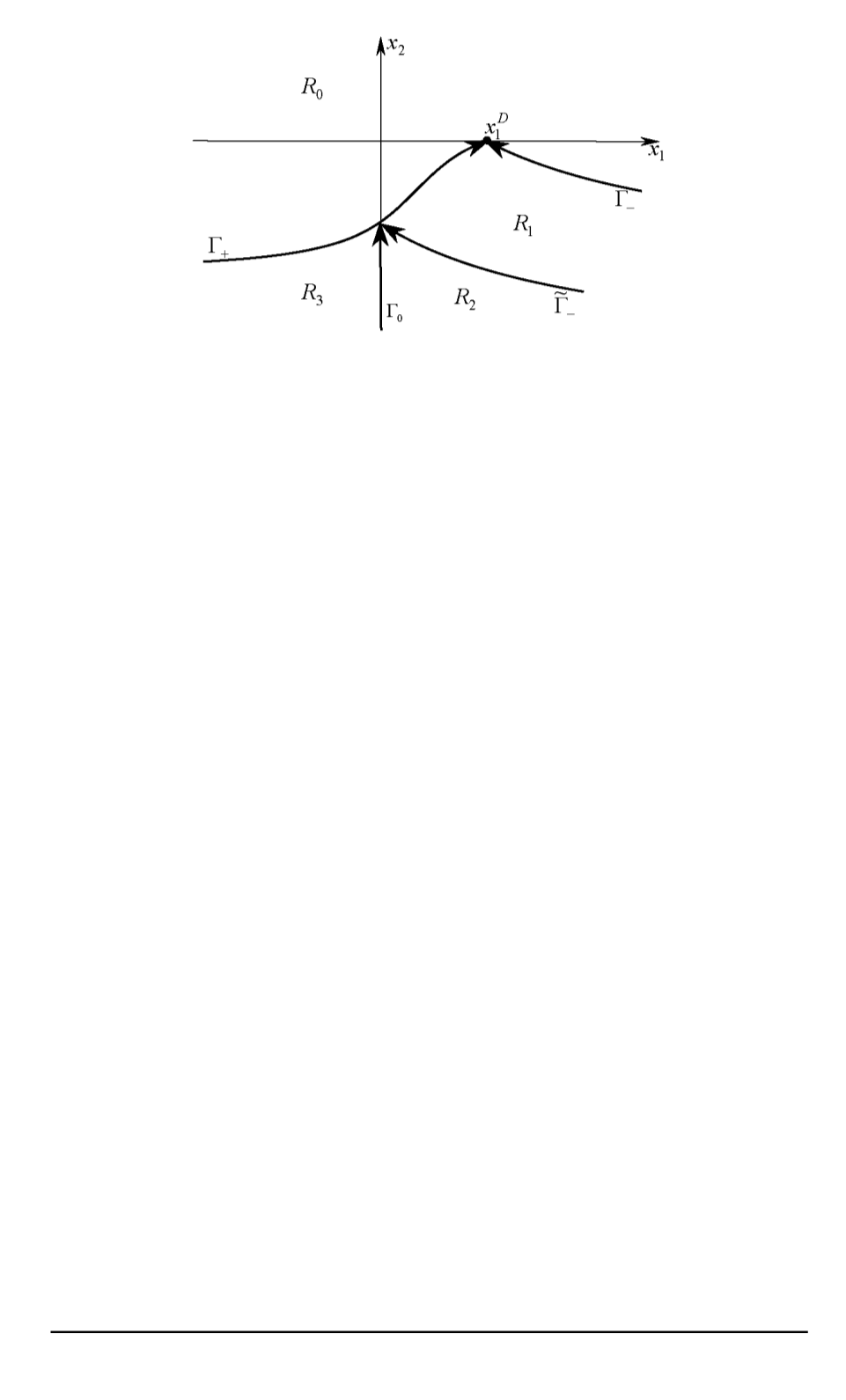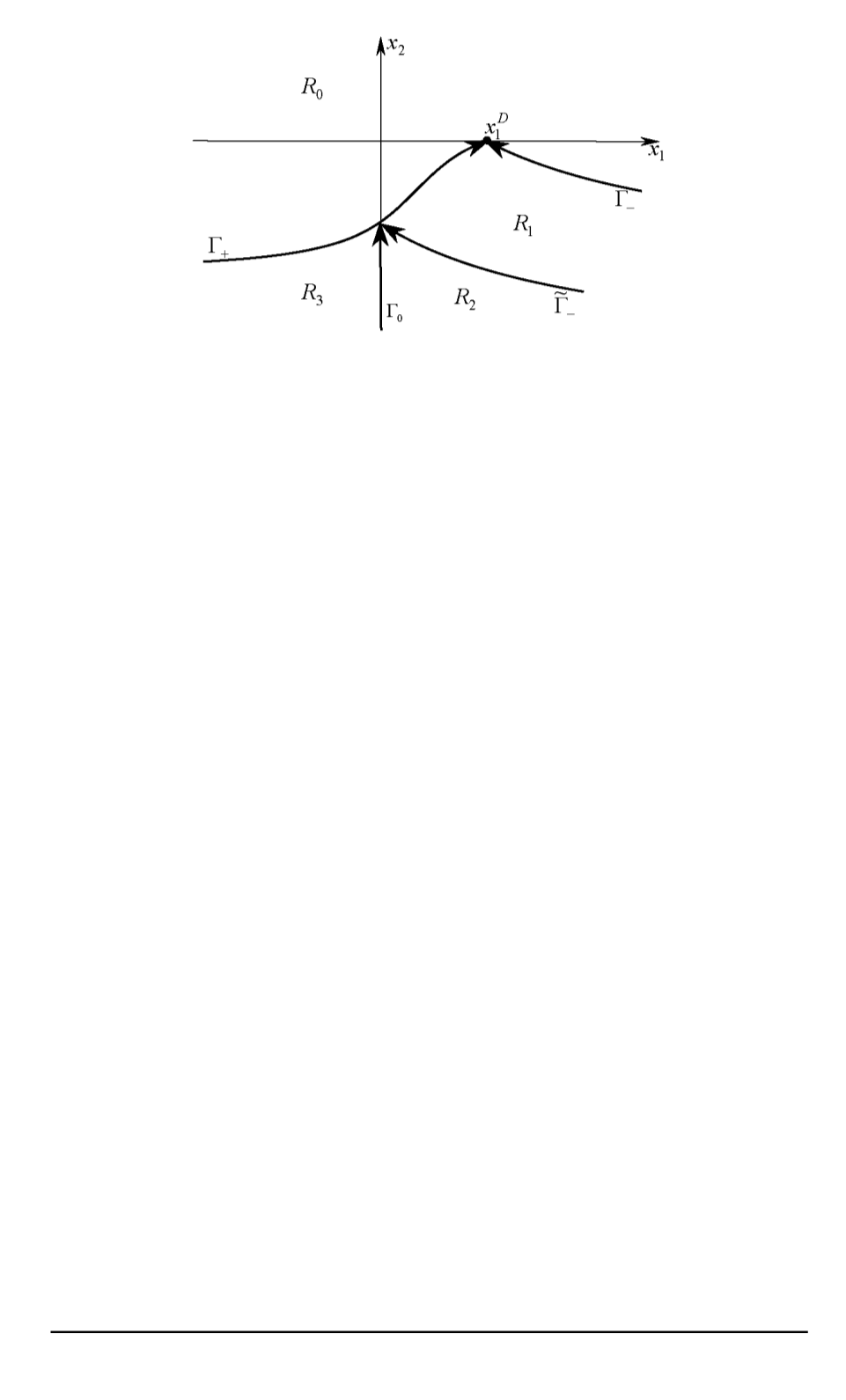
Рис. 2. Области на фазовой плоскости в задаче быстродействия
Не нарушая общности, можно положить, что в конечный момент
времени расстояние между телами положительно, т.е.
x
D
1
=
l
D
>
0
.
Утверждение 2.
Если
x
D
1
>
0
и в начальный момент времени
система не лежит в области
R
0
, то оптимальный закон управления
имеет вид
u
=
−
u
m
при
(
x
1
,
x
2
)
2
R
1
∪
R
2
∪
0
−
∪ ˜
0
−
,
+
u
m
при
(
x
1
,
x
2
)
2
R
3
∪
0
+
,
0
при
(
x
1
,
x
2
)
2
0
0
.
(16)
Если система находится в области
R
1
, то оптимальная управляющая
последовательность имеет вид
{−
u
m
,
u
m
}
. Если система находится в
области
R
2
, то оптимальной управляющей последовательностью явля-
ется
{−
u
m
,
0
,
u
m
}
. Если система находится в области
R
3
, то оптималь-
ная управляющая последовательность
u
= {
u
m
,
0
,
u
m
}
.
Доказательство утверждения 2 приведено в работе [17].
Соответствующие оптимальные фазовые траектории при различ-
ных начальных условиях показаны на рис. 3.
Механический смысл оптимального решения очевиден. При умень-
шении момента инерции связки двух тел относительно их общего
центра масс увеличивается угловая скорость вращения в силу закона
сохранения кинетического момента. На оптимальной траектории не-
обходимо с максимально возможной скоростью сближать тела и тем
самым уменьшать момент инерции связки тел относительно обще-
го центра масс, а затем удалять тела одно от другого на требуемое
конечное расстояние между ними тоже с максимально возможной ско-
ростью. Если при этом удается достичь положения с минимальным
моментом инерции (когда совпадают центры масс этих тел), то следу-
ет оставаться в этом положении как можно дольше.
24
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4