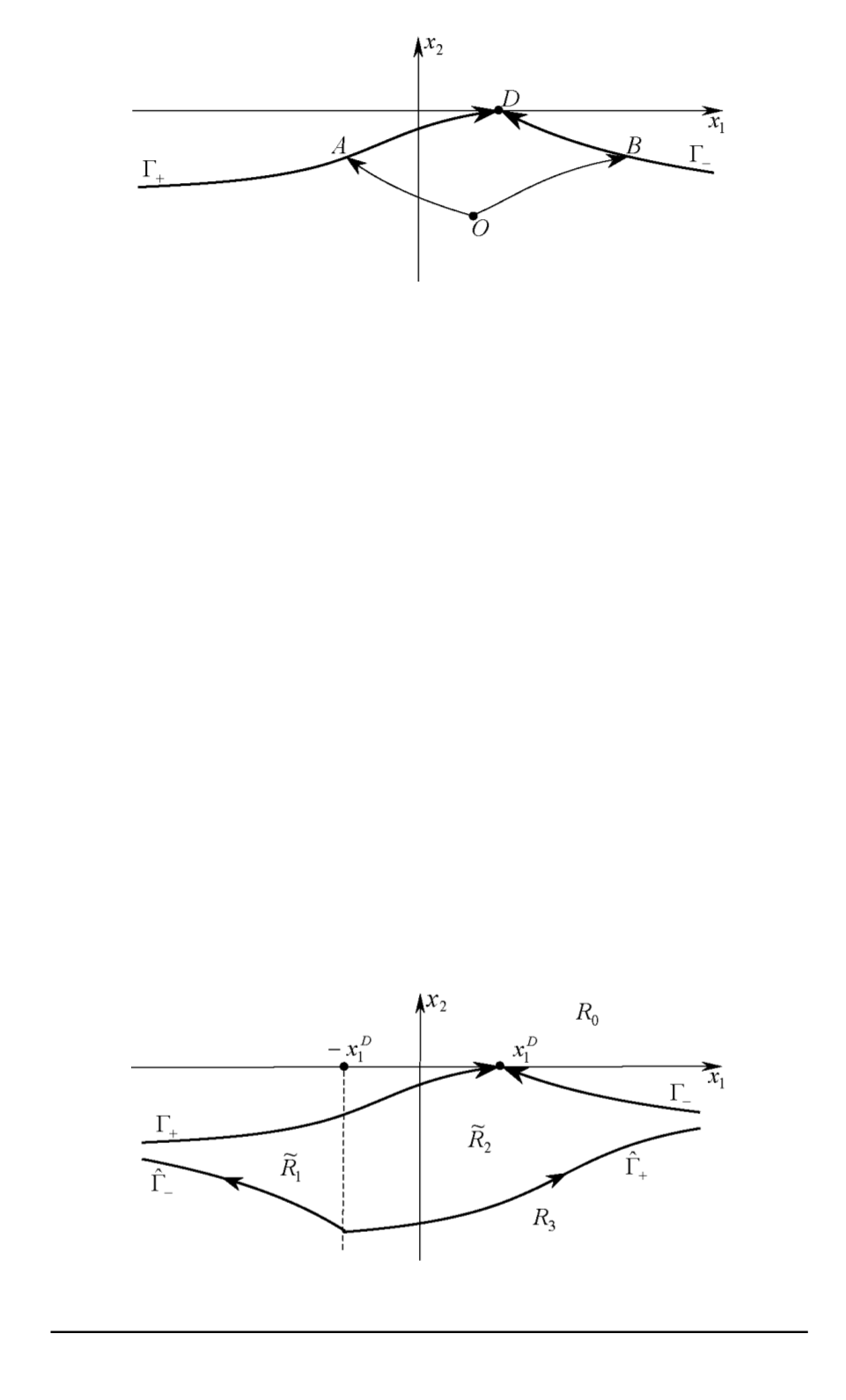
Рис. 4. Два типа экстремальных фазовых траекторий
щая последовательность
{−
u
m
,
u
m
}
; решения типа
B
— траектория
OBD
, управляющая последовательность
{
u
m
,
−
u
m
}
.
Рассмотрим две фазовые траектории:
ˆ
0
+
, соответствующую упра-
влению
u
=
u
m
, и
ˆ
0
−
, соответствующую управлению
u
= −
u
m
, при-
чем
ˆ
0
+
и
ˆ
0
−
имеют одинаковые горизонтальные асимптоты соответ-
ственно с
0
−
и
0
+
.
Если начальное положение системы
(
x
1
,
x
2
)
находится на
ˆ
0
+
или
ниже нее, то точка
B
— бесконечно удаленная и время движения по
траектории типа
B
бесконечно большое. Аналогично, если начальное
положение системы
(
x
1
,
x
2
)
находится на
ˆ
0
−
или ниже нее, то время
движения по траектории типа
A
бесконечно большое.
Линии
0
+
,
0
−
,
ˆ
0
+
,
ˆ
0
−
и прямая
x
1
= −
x
D
1
делят фазовую плоскость
на четыре области:
R
0
,
˜
R
1
,
˜
R
2
,
R
3
(рис. 5).
Если в начальный момент времени система находится в области
R
0
, ее невозможно перевести в требуемое конечное положение (утвер-
ждение 1). Если в начальный момент времени система находится в
области
R
3
(включая границу), то ее можно перевести в требуемое
конечное положение за сколь угодно большое время.
Утверждение 3.
Если
x
D
1
>
0
и в начальный момент времени
система не лежит в области
R
0
∪
R
3
, то оптимальный закон управления
Рис. 5. Области на фазовой плоскости в задаче максимизации времени
разворота
26
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


