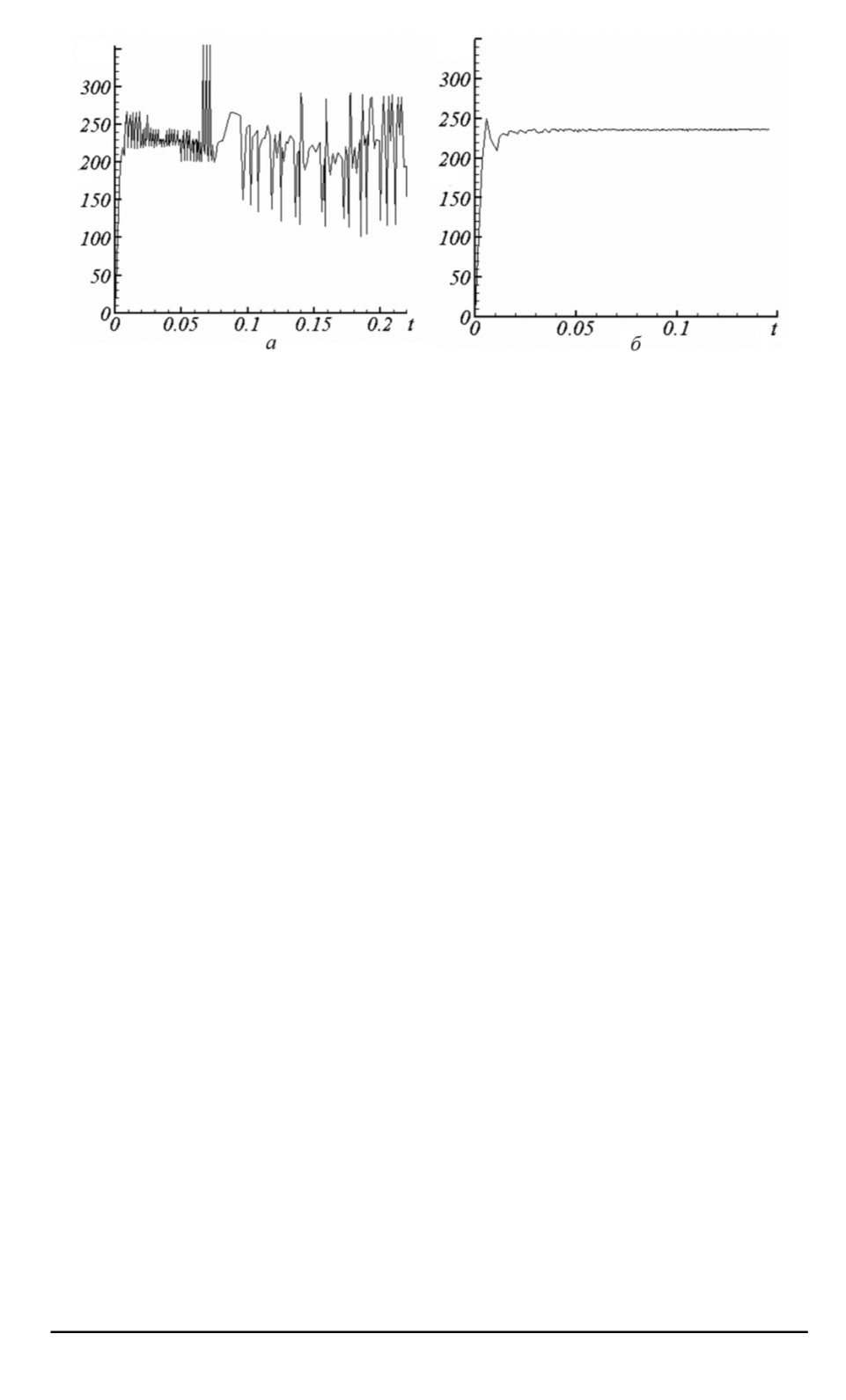
Рис. 7. Среднее число внутренних итераций без явного (
а
) выделения особенно-
сти и с явным (
б
) выделением, сетка 3
При таком задании
A
0
выполняются требования: div
A
0
=
0
и
rot
A
0
=
0
в диэлектрической подобласти.
На внешних итерациях для вычисления
A
строится система
M
A
=
f
−
M
A
0
. Здесь
M
— матрица, аппроксимирующая на раз-
ностной сетке симметричную часть оператора системы уравнений
Максвелла;
f
— правая часть системы, к которой на внутренних итера-
циях относятся конвективные слагаемые. После получения
A
вычи-
сляется
A
=
A
+
A
0
. Такое изменение правой части системы помогает
стабилизировать среднее число итераций, необходимых для решения
системы методом сопряженных градиентов. После добавления к пра-
вой части системы слагаемого
(
−
M
A
0
)
и добавления к
A
слагаемого
A
0
суммарная погрешность в вычислении вектора
A
увеличивается.
Для улучшения сходимости внешних итераций достаточно повысить
точность в критериях прекращения внутренних итераций. Среднее
число итераций, необходимых для решения системы методом сопря-
женных градиентов для сетки 3 с повышенной точностью в критериях
прекращения внутренних итераций, представлено на рис. 7. На рис. 8
приведена зависимость параметра
κ
от времени, а на рис. 9 — вид
решения
A
для сетки 3.
Некоторые дополнительные подробности выполненной работы
приведены в [16].
Выводы.
Исследовано влияние калибровки математической моде-
ли и разностных эффектов (формы разностных операторов) на по-
явление экстремумов, отражающих особенность решения. Модель с
измененной калибровкой позволяет увеличить шаг по времени, не-
обходимый для выполнения условий сходимости итераций с учетом
конвективных слагаемых. При изменении формы разностных опера-
торов устраняются экстремумы, обусловленные особенностью реше-
ния вблизи угловой точки. После проведения преобразований модель
54
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


