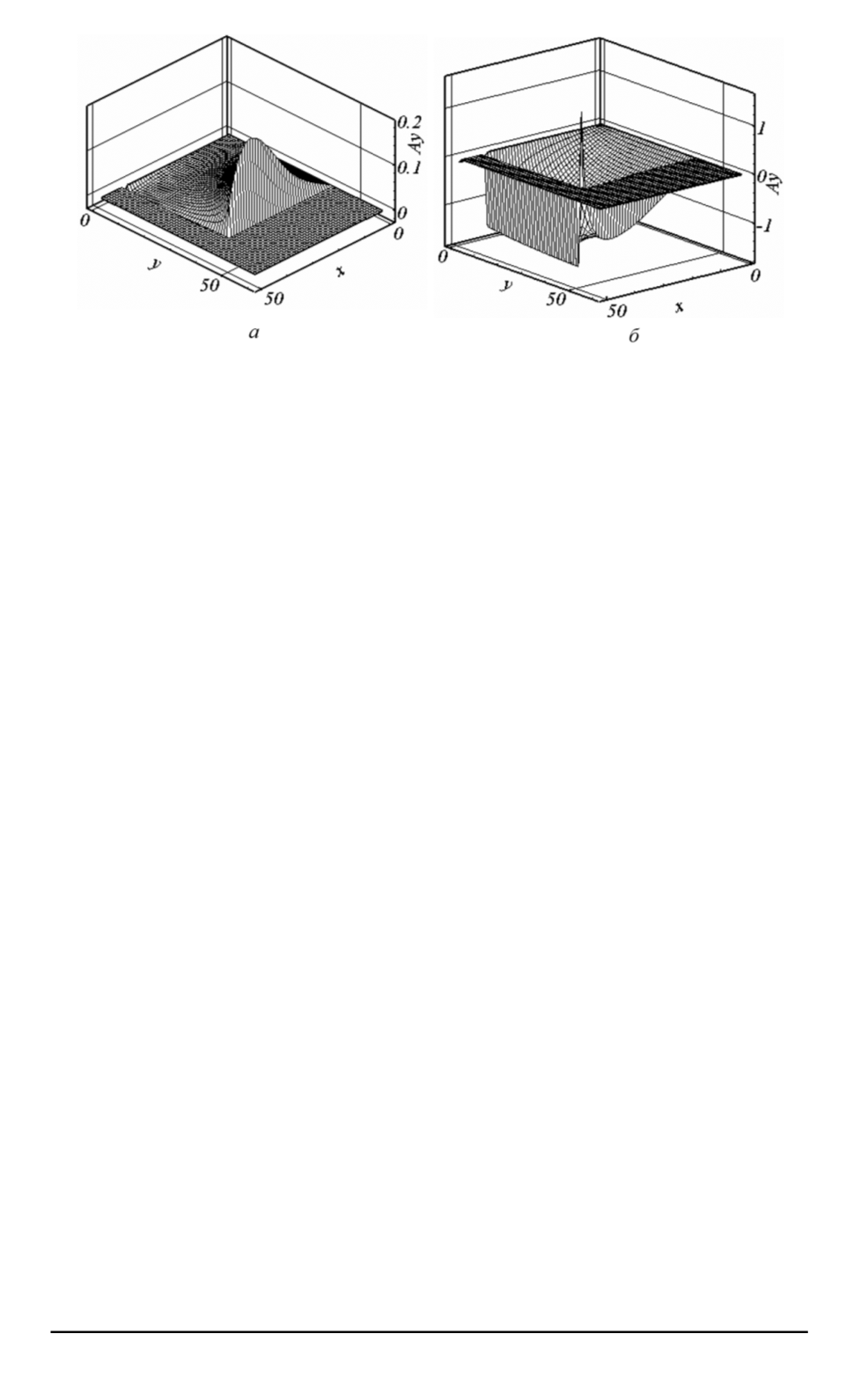
Рис. 2. Решение для случая калибровки
φ
=
0
;
t
=
0
,
395
, сетка 3
ток
I
(
t
)
=
I
max
t
/
t
0
exp
(
1
−
t
/
t
0
)
, параметры в критериях прекращения
итераций, сетка и т.д.) для всех расчетов (с различной калибровкой)
берутся одинаковыми.
На рис. 2,
a
представлено решение для случая калибровки
φ
=
0
,
a на рис. 2,
б
— решение с измененной калибровкой
φ
= −
(
v
,
A
)
на
тот же момент времени. Вдоль осей для наглядности расположены
номера ячеек (координаты диэлектрической подобласти, в которой ис-
следуются особенности решения для сетки 3: по оси
x
0–50, по оси
y
0–50).
При изменении калибровки в угловой точке возникает экстремум
решения (см. рис. 2,
б
). Причиной появления экстремума в рассматри-
ваемом случае может являться выбранный способ разностной аппрок-
симации дифференциальных операторов.
Аппроксимация векторного произведения [
w
,
H
] в [1] представля-
ет собой форму, переводящую векторные сеточные функции, задава-
емые своими компонентами на гранях ячеек, и векторные сеточные
функции, относящиеся к вершинам, в векторные сеточные функции,
задаваемые своими компонентами на ребрах ячеек. Для лучшей ап-
проксимации такая форма должна включать в себя полусумму соста-
вляющих вектора
H
по граням, прилегающим к ребру, но это приводит
к немонотонности решения [1].
Для обеспечения монотонности решения произведение [
w
,
H
] в [1]
берется в виде
[
w
,
H
]
3
,
x
=
1
/η
x
,
i
(
h
x
,
i
+1
,
i
w
i
+1
,
j
+
h
x
,
i
,
i
w
i
,
j
)
H
z
,
i j
(5)
(здесь
η
x
,
i
— длина ребра сетки,
h
x
,
i
,
i
— расстояние от центра ребра до
вершины). В этом случае при калибровке
φ
= −
(
v
,
A
)
конвективное
слагаемое будет входить в уравнение для
A
x
в якоре вблизи угловой
точки, что нарушает однотипность уравнений вдоль границы раздела
50
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4


