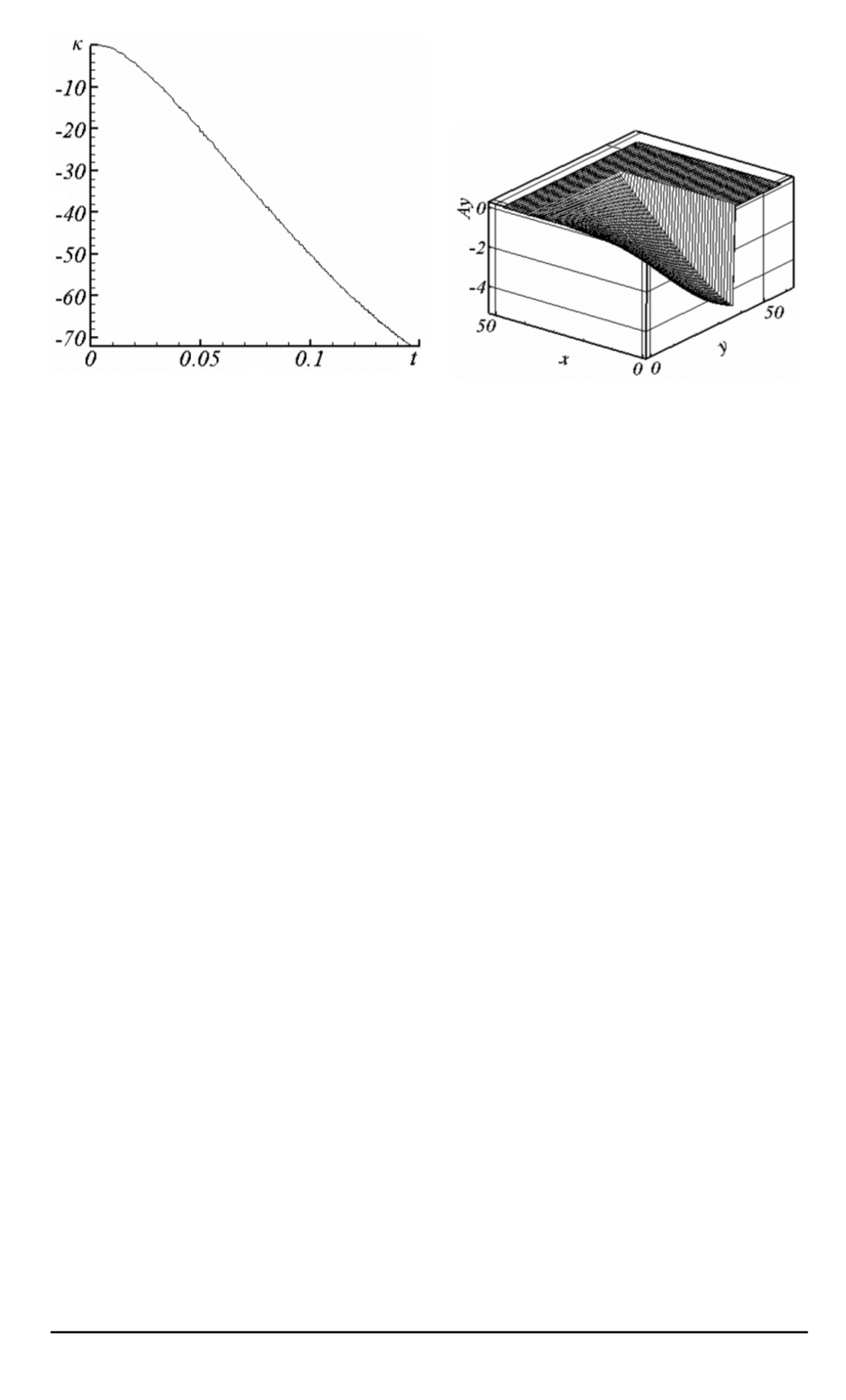
Рис. 8. Зависимость параметра
κ
от вре-
мени
t
=
0
,
150
, сетка 3
Рис. 9. Вид решения A для сетки 3
остается однородной по пространству. Явное выделение особенно-
сти решения позволяет стабилизировать число внутренних итераций,
но не изменяет способа учета конвективных слагаемых при решении
системы линейных алгебраических уравнений и вследствие этого не
может существенно увеличить шаг по времени, необходимый для схо-
димости внешних итераций.
СПИСОК ЛИТЕРАТУРЫ
1. Г а л а н и н М. П., П о п о в Ю. П. Квазистационарные электромагнитные
поля в неоднородных средах: Математическое моделирование. – М.: Физматлит,
1995. – 320 с.
2. В о л к о в Е. А. О дифференциальных свойствах решений краевых задач для
уравнений Лапласа и Пуассона в прямоугольнике // Тр. МИАН СССР. – 1965. –
Т. 77. – С. 89–112.
3. В о л к о в Е. А. Об устранении особенностей при решении краевых задач для
уравнения Лапласа в областях с гладкой границей // ЖВМ и МФ. – 1963. – Т. 3.
– № 1. – С. 109–119.
4. К о н д р а т ь е в В. А. Краевые задачи для эллиптических уравнений в обла-
стях с коническими или угловыми точками // Тр. Моск. мат. о-ва. – 1967. – Т. 16.
– С. 209–292.
5. К о н д р а т ь е в В. А., К о п а ч е к И., О л е й н и к О. А. О поведении
обобщенных решений эллиптических уравнений второго порядка и системы те-
ории упругости в окрестности граничной точки // Тр. сем. им. И.Г. Петровского.
– 1982. – Т. 8. – С. 135–152.
6. Ф р я з и н о в И. В. Разностные схемы для уравнений Лапласа в ступенчатых
областях // ЖВМ и МФ. – 1978. – Т. 18, № 5. – С. 1170–1185.
7. Ф и к е р а Г. Асимптотическое поведение электрического поля и плотности
электрического заряда в окрестности сингулярных точек проводящей поверх-
ности // Успехи мат. наук. – 1975. – Т. 30, вып. 3(183). – С. 105–124.
8. Б о р с у к М. Вырождающиеся эллиптические краевые задачи второго поряд-
ка в негладких областях // Современная математика. Фундаментальные направ-
ления. – 2005. – Т. 13. – С. 3–137.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4
55


