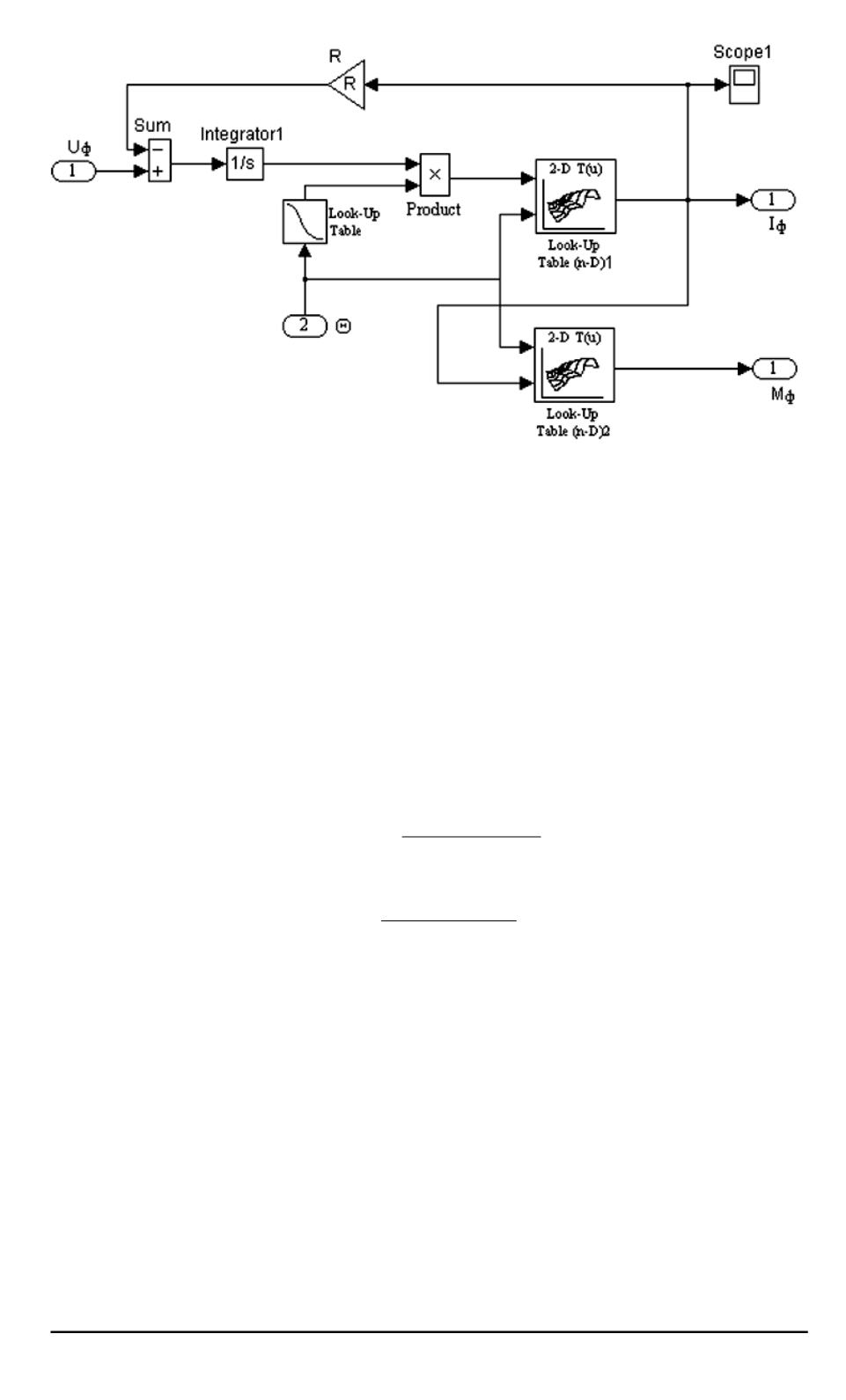
Рис. 6. Схема формирования фазных тока и момента в модели
IMTF
с исполь-
зованием таблично заданных нелинейных магнитных характеристик ВИМ
иметь нелинейную модель ВИМ с возможностью гибкого изменения ее
геометрических параметров, свойств используемых материалов и т.п.,
необходимо при построении модели использовать другие подходы.
Расчеты на основе универсальных нормированных кривых
Миллера.
Т. Миллером в работах [7, 8] установлено, что если кривые
намагничивания ВИМ представить в виде зависимостей
9(2)
для ря-
да значений фазного тока
I
ф
, как на рис. 7,
а
, где показаны кривые для
четырех значений тока (
I
1
<
I
2
<I
3
<I
4
)
, а затем их соответствующим
образом нормировать, используя выражения
y
(
x
)
=
9 (
x
)
−
9
min
9
max
−
9
min
(11)
и
x
=
2
−
2
min
2
max
−
2
min
,
(12)
то полученные зависимости
y
(
x
) при различных значениях
I
ф
прак-
тически совпадают. Здесь
9
max
— потокосцепление в положении ро-
тора
2
max
(см. рис. 1),
9
min
— потокосцепление в положении ротора
2
min
;
9
(
x
) — потокосцепление в промежуточном положении ротора
x
. Отметим, что в выражении (11) потокосцепления
9
,
9
max
,
9
min
определяются при одном и том же значении тока.
Усредненная кривая
y
(
x
), вид которой показан на рис. 7,
б
, по-
лучила в литературе название кривой Миллера. Координаты
x
рас
,
x
согл
на рис. 7,
б
определяются из выражения (12) соответственно при
2
=
2
рас
и
2
=
2
согл
. На основе зависимости
y
(
x
), которая, по сути,
с некоторым приближением отражает особенности геометрии магнит-
ной системы конкретного экземпляра ВИМ, можно установить вид
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2007. № 4
69


