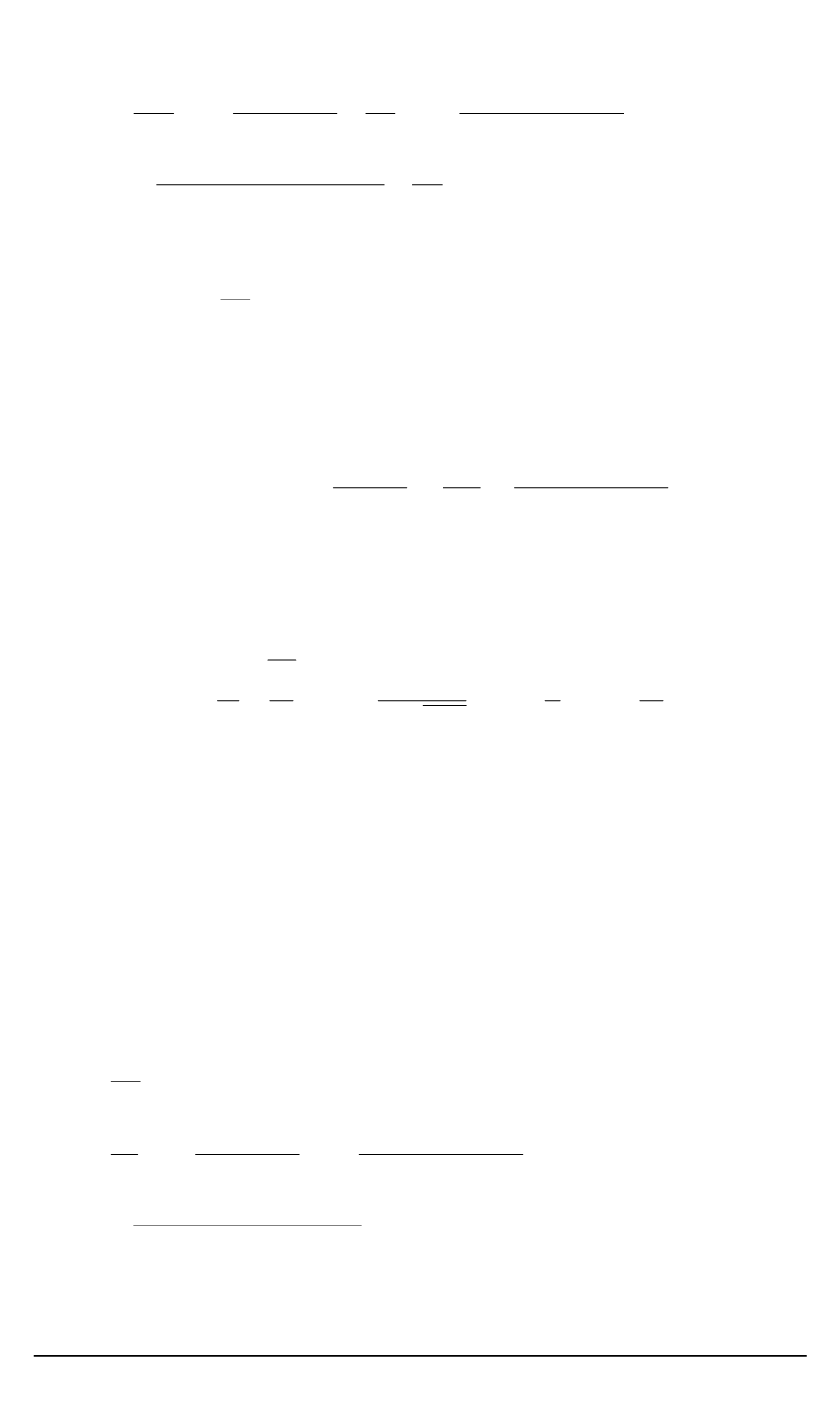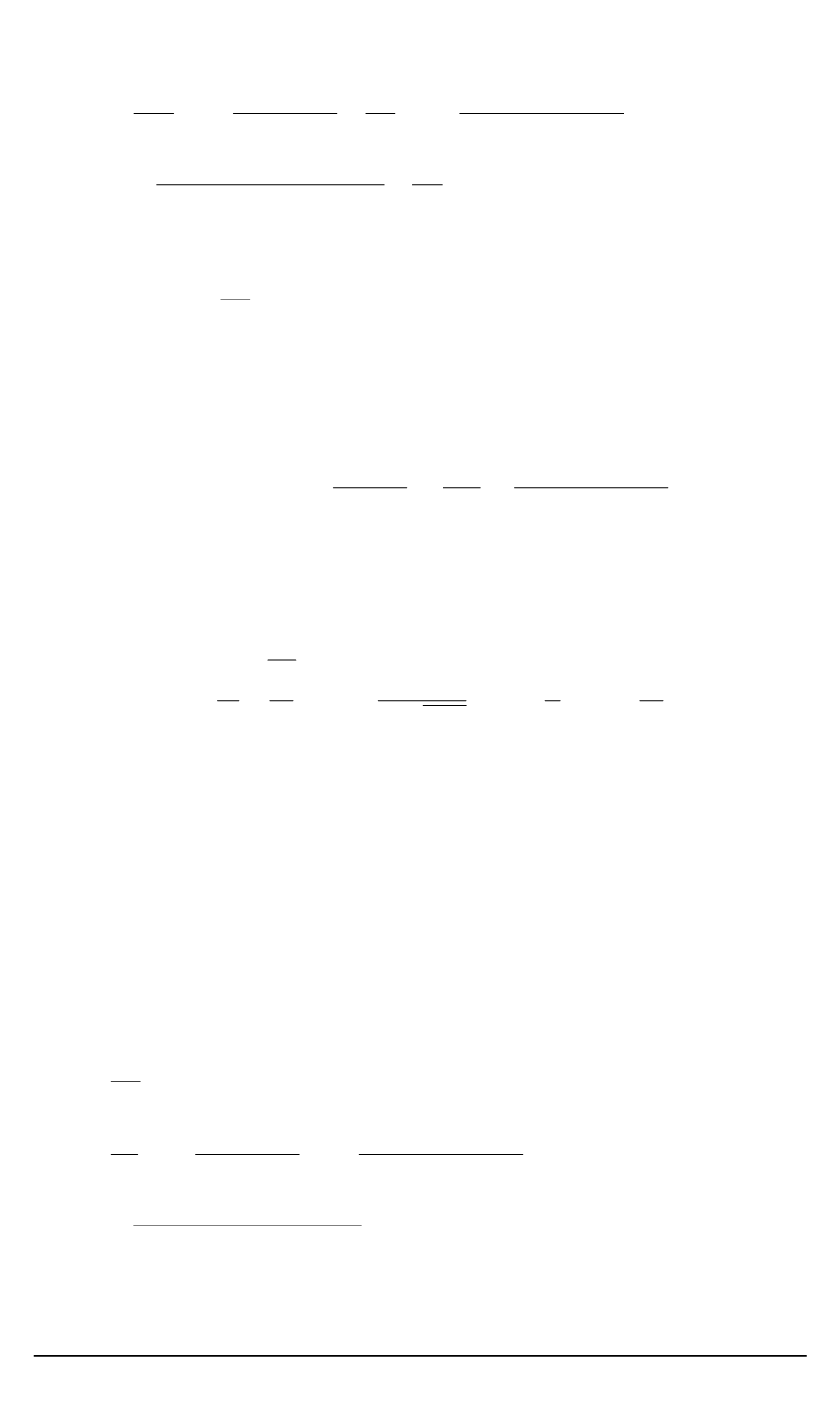
филя в изучаемой системе, имеет вид:
d
2
α
dξ
2
=
(
B
(
α, δ, γ
)
6
dα
dξ
2
+
4
kR
(
α
0
−
1)
2
/
3
3(
α
−
1)
×
×
(
α
−
1)(1
−
δ
) +
ζαδ
δ
+
α
−
1
dα
dξ
−
F
(
α, α
0
, δ, γ, k
)
×
×
A
−
1
(
α, δ, γ
)
, ξ >
0;
9
lim
ξ
→
+
∞
dα
dξ
= 0;
9
lim
ξ
→
+
∞
α
=
α
0
,
(4)
где
F
(
α, α
0
, δ, γ, k
) =
α
(
α
0
−
1)
2
/
3
×
×
[1 + (
γ
−
1)
δ
]
α
0
−
α
α
2
0
+
2
k
2
3
ln
α
0
(
δ
+
α
−
1)
α
(
δ
+
α
0
−
1)
;
α
2
[1
, α
0
];
ζ
2
R
+
;
γ
2
R
+
; 0
< δ
≤
1;
(5)
и структура функционалов
A
(
α, δ, γ
)
и
B
(
α, δ, γ
)
известна [4].
В математической модели (4), (5)
k
=
1
D
s
Y
ρ
1
;
R
=
η
a
0
√
Y ρ
1
;
ζ
=
μ
η
;
γ
=
ρ
2
ρ
1
;
η, μ
— коэффициенты вязкости фаз 1 и 2 соответственно; индекс “0”
относится к начальным значениям величин.
Системы алгебраических уравнений для определения точек
покоя системы (4), (5).
Для достижения цели исследования удобнее
ввести новое переменное
g
Δ
=
dα
/
dξ.
(6)
В этом случае
d
2
α
/
dξ
2
=
dg
/
dξ
и, согласно (4), (5), приходим к
нормальной системе обыкновенных дифференциальных уравнений
dα
dξ
=
g
;
dg
dξ
=
B
(
α, δ, γ
)
6
g
2
+
4
kR
(
α
0
−
1)
2
/
3
3(
α
−
1)
×
×
(
α
−
1)(1
−
δ
) +
ζαδ
δ
+
α
−
1
g
−
F
(
α, α
0
, δ, γ, k
)
A
−
1
(
α, δ, γ
)
.
(7)
В фазовой плоскости
α
0
g
точки покоя изучаемой системы, пред-
ставленной математической моделью (4), (5), определяются как корни
98
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2