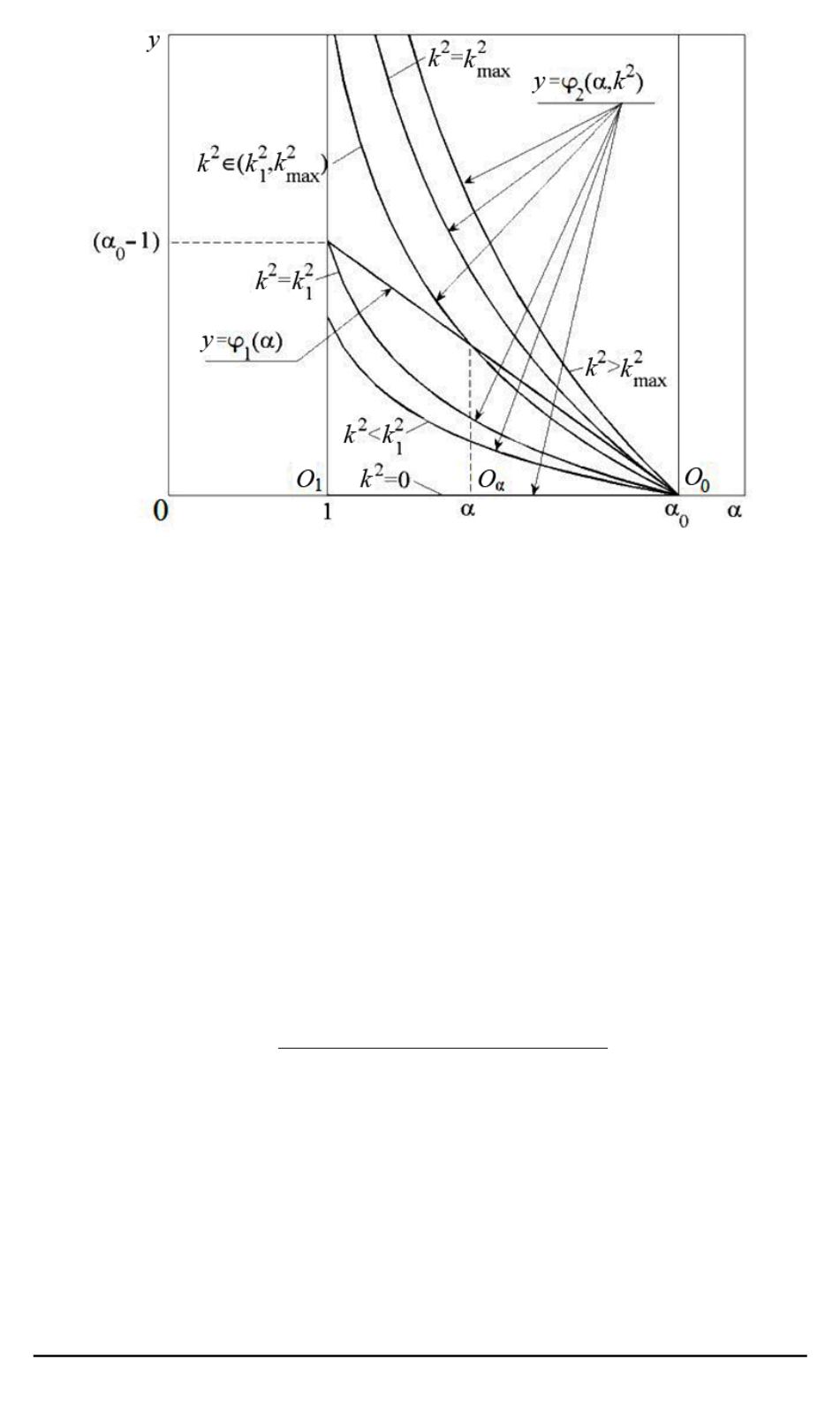
Рис. 2. Зависимость положения третьей точки покоя изучаемой системы от
значения бифуркационного параметра
k
покоя
O
α
= (
α,
0)
(рис. 2), где
α
2
(1
, α
0
)
,
а значения
k
2
1
и
k
2
max
опреде-
лены равенствами (14) и (17) соответственно. Кроме того, при
k
2
< k
2
1
система (8) определяет единственную точку покоя
O
0
= (
α
0
,
0)
. При
k
2
=
k
2
1
появляется вторая точка покоя
O
1
= (1
,
0)
,
которая с ро-
стом значения параметра
k
2
начинает “перемещаться” по отрезку, со-
единяющему точки
(1
, α
0
−
1)
и
(
α
0
,
0)
,
от точки
(1
, α
0
−
1)
к точке
(
α
0
,
0)
.
При
k
2
=
k
2
max
эта вторая точка покоя “попадает” в точку покоя
O
0
= (
α
0
,
0)
; при дальнейшем росте параметра
k
2
данная точка исче-
зает из зоны анализа. Значение параметра
k
2
max
, определенного равен-
ством (17), где функционал
ϕ
(
γ, δ
)
задан последним равенством (16),
устанавливает условие существования минимальной скорости распро-
странения УВ в двухфазном пористом материале:
D
min
=
2
Y α
0
(1
−
δ
)
3
ρ
1
(
δ
+
α
0
−
1) [1 + (
γ
−
1)
δ
]
1
/
2
.
(18)
Ее появление физически обусловлено проявлением механических
свойств фазы 1 изучаемого материала. При
δ
= 0
равенство (18)
известно [1, 2].
Классификация точек покоя.
Согласно (5), система (9) определя-
ет единственную точку покоя
O
1
= (1
,
0)
,
которая всегда существует
безотносительно к значениям определяющих безразмерных параме-
тров системы. При этом параметр
k
2
является бифуркационным па-
раметром. Действительно, при
k
2
2
(0
, k
2
1
)
∪
(
k
2
max
,
+
∞
)
изучаемая
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2013. № 2
101


