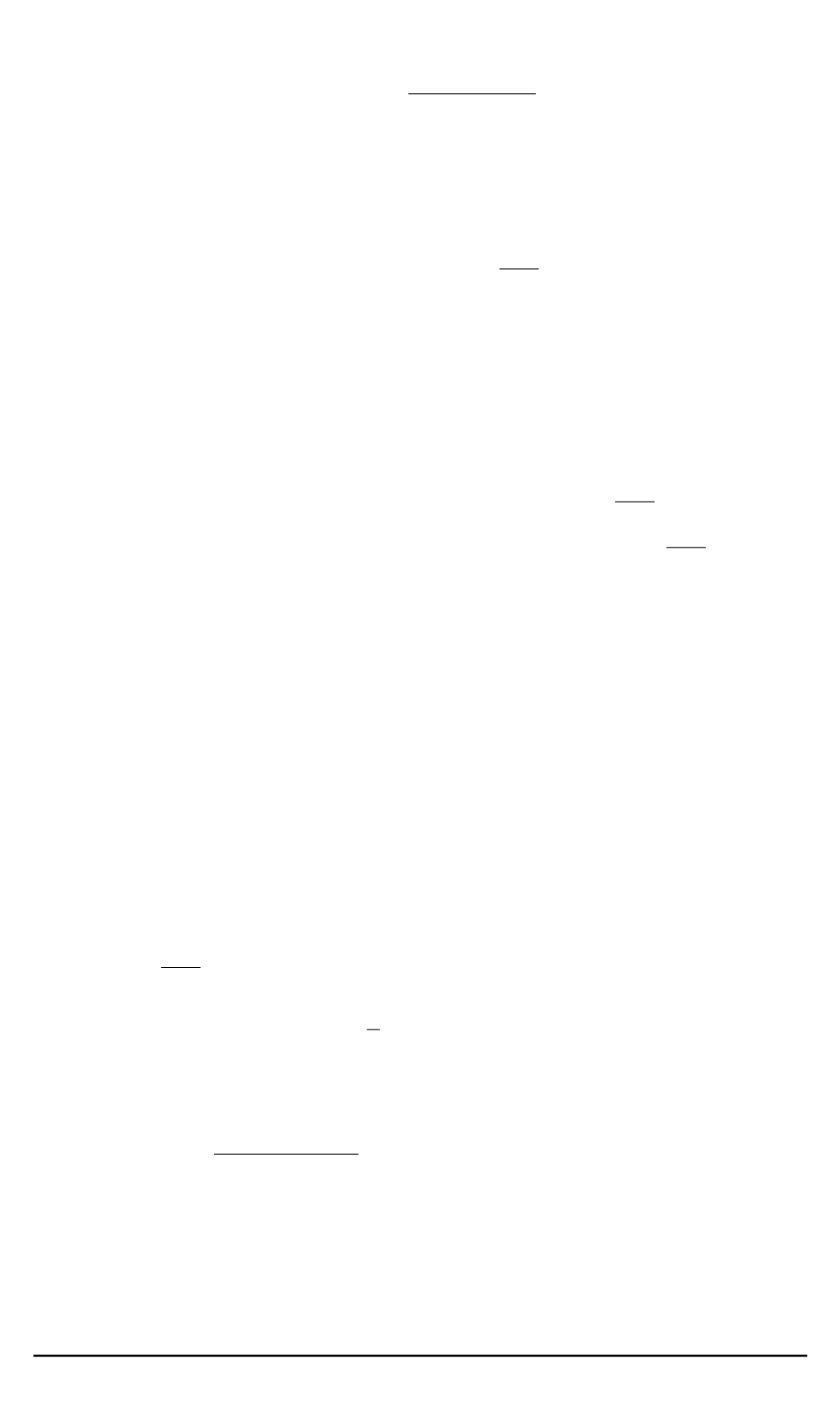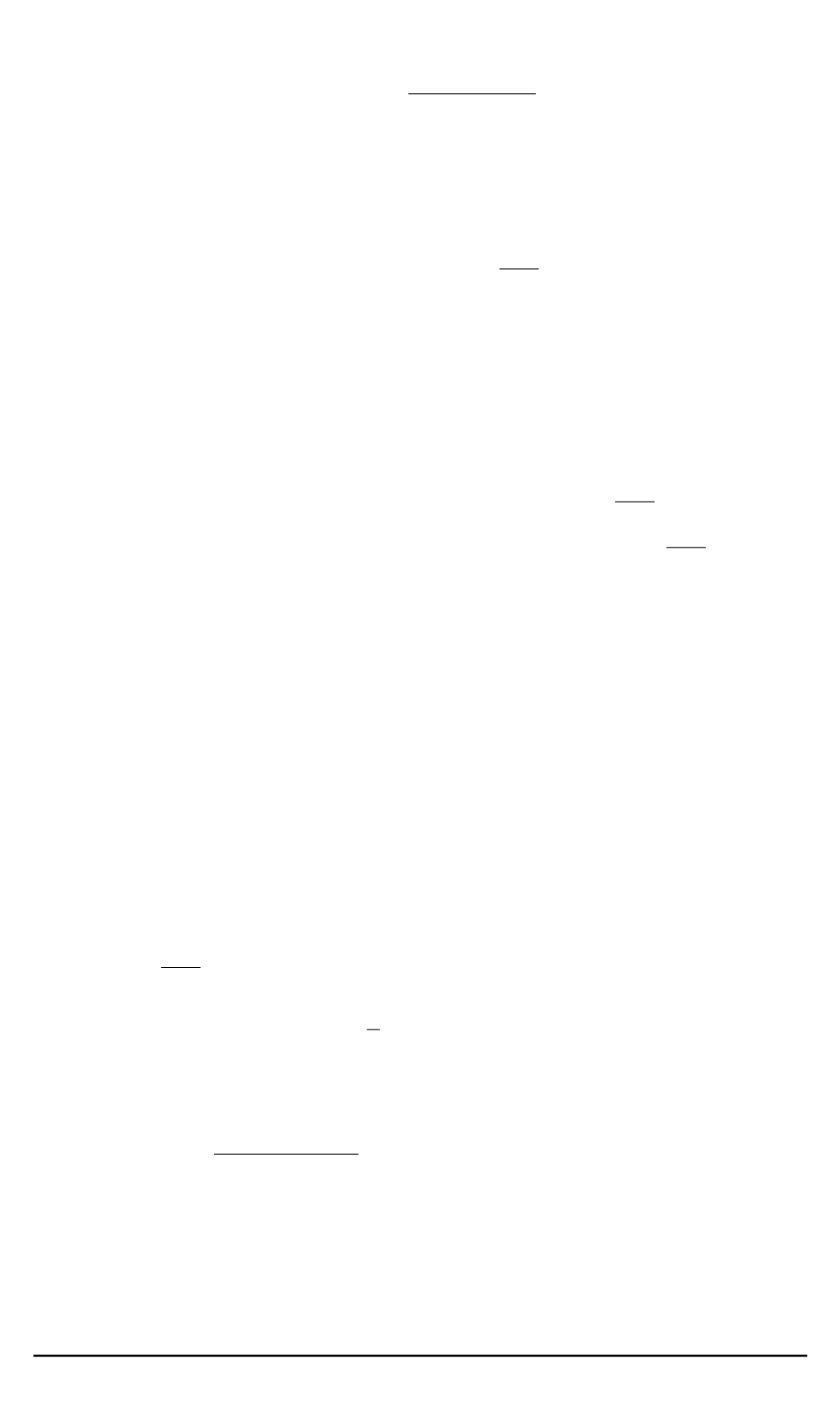
то приближенно
Var
h
◦
θ
i
=
σ
2
r
0
θ
(
X, θ
)
2
.
Состоятельная оценка регрессионного коэффициента.
Пусть
выполняются условия (1)–(3) и имеются результаты
n
независимых
наблюдений значений фактора
X
i
и отклика
y
i
=
Y
i
+
ε
i
, i
= 1
, n,
(4)
где
ε
i
— реализации случайной величины
ε
.
Обозначим
◦
θ
=
◦
θ
1
,
◦
θ
2
, . . . ,
◦
θ
n
,
где
◦
θ
i
— значения регрессионного коэффициента
θ
, реализующие функ-
цию регрессии
Y
=
r
(
X, θ
)
в точках
(
X
i
, y
i
)
,
i
= 1
, n
. Получить
◦
θ
i
можно, решив систему уравнений
y
i
=
r X
i
,
◦
θ
i
,
i
= 1
, n
, относи-
тельно
◦
θ
i
. Необходимо обратить внимание на то, что в общем слу-
чае решение каждого из уравнений этой системы является не един-
ственным. На практике получить единственное решение можно, сузив
область возможных значений
◦
θ
i
, “. . . исходя из условий конкретной
задачи” [6].
Пусть
◦
ˉ
θ
:=
n
−
1
n
X
i
=1
◦
θ
i
(5)
— среднее значение ряда
◦
θ
.
Теорема 3.
При выполнении условий
(
1–3
)
,
а в каждой точке
(
X
i
, θ
)
,
i
= 1
, n
,
условий
(
4
)
и условий
теоремы 2
˜
θ
=
◦
θ
−
n
−
1
n
X
i
=1
W
i
(6)
является состоятельной оценкой регрессионного коэффициента
θ
.
Здесь
W
i
=
−
σ
2
r
00
θθ
(
X
i
, θ
)
2 (
r
0
θ
(
X
i
, θ
))
3
.
Доказательство.
Для доказательства состоятельности оценки
˜
θ
регрессионного коэффициента
θ
воспользуемся следующей теоремой:
если оценка
˜
θ
параметра
θ
— несмещенная и
Var
h
˜
θ
i
→
0
при
n
→ ∞
,
то
˜
θ
— состоятельная оценка параметра
θ
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
7