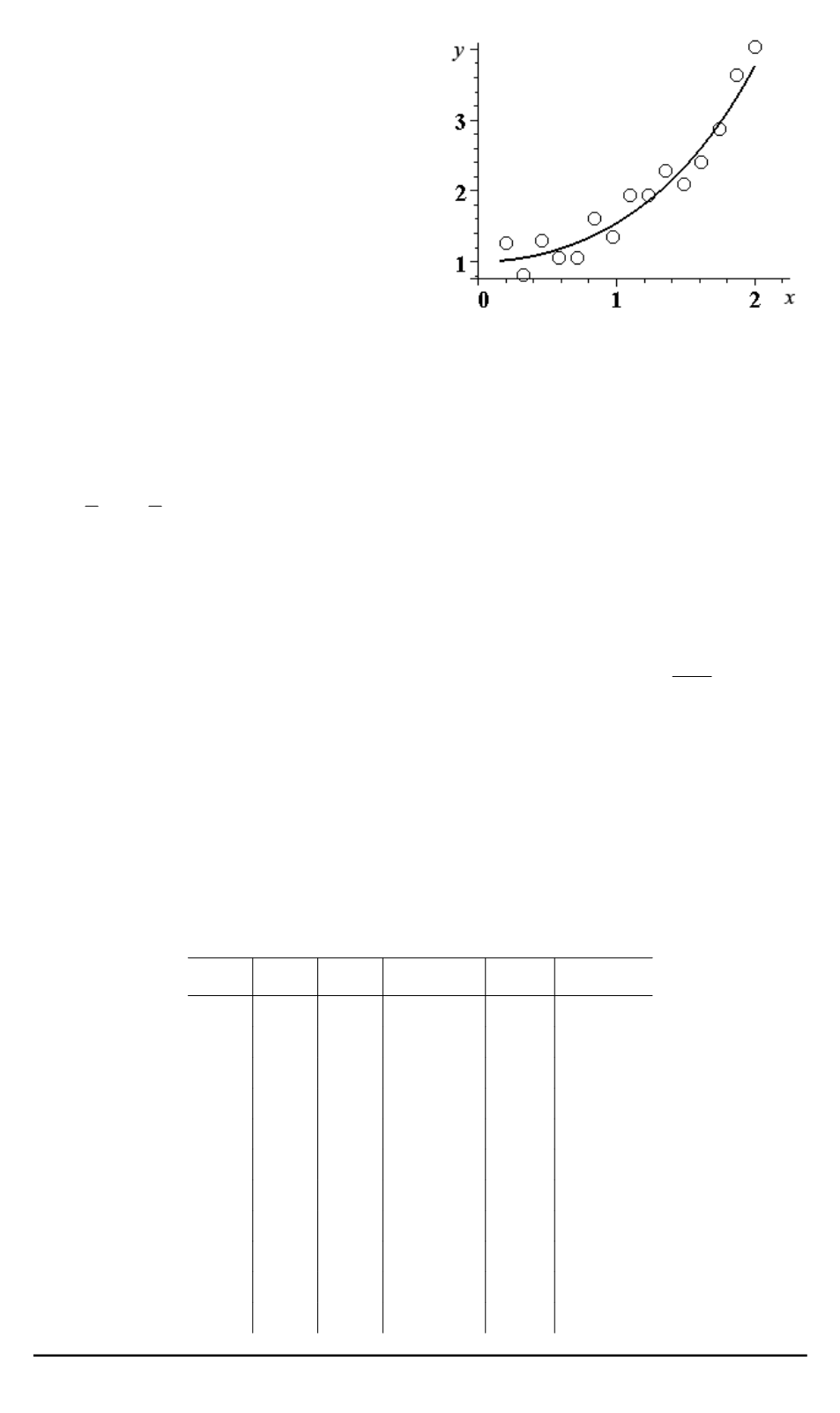
Рис. 1. Модель значений фактора и
отклика:
——– — линия регрессии
Y
=
r
(
X, θ
)
;
◦
— точки с координатами
(
X
i
, y
i
)
, где
y
i
=
Y
i
+
ε
i
математических символьных вычи-
слений Maple. Модель значений от-
клика строилась по формуле (2).
Регрессия задавалась функцией ви-
да
r
(
X, θ
) = ch (
X/θ
)
при значении параметра
θ
= 1
, за-
данной на интервале
@
= (0
,
2
,
2)
.
Моделирование погрешности
отклика
ε
осуществлялось про-
граммой random статистического
пакета Stats системы Maple. Зна-
чения
ε
строились как элемен-
ты выборки объема
n
равномерного распределения на интервале
− √
3
σ,
√
3
σ
,
σ
= 0
,
202
. На рис. 1 изображен один из результатов
моделирования.
В таблице приведены результаты эксперимента оценивания по фор-
мулам (5), (6). Значения первого столбца соответствуют номеру экс-
перимента. Значения
N
соответствуют количеству найденных зна-
чений
◦
θ
i
как решений уравнений
y
i
=
r x
i
,
◦
θ
i
,
i
= 1
, n
в обла-
сти
Θ = [
θ/
10
,
2
θ
]
предполагаемых значений
θ
. Уравнения реша-
лись численным методом половинного деления, программно реали-
зованным в среде Maple. Значения
N
0
соответствуют количеству зна-
чений
◦
θ
i
, для которых выполняются условия
теоремы 1
. Значения
ε
◦
ˉ
θ
=
◦
ˉ
θ
−
θ
соответствуют абсолютной погрешности оценки по фор-
№
n N ε
◦
ˉ
θ
N
0
ε
˜
θ
1 4
3 0,2309 2 0,0199
2 6
5 0,0603 3 0,0408
3 9
7 0,0090 5 0,0029
4 11 8 0,1841 5 0,0462
5 15 13 0,0277 9 0,0135
6 18 14 0,0513 10 0,0246
7 20 17 0,056 10 0,0007
8 26 21 0,0631 13 0,0005
9 31 22 0,0075 18 0,0058
10 41 33 0,0161 23 0,0146
11 51 49 0,0524 30 0,0111
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3
9


