муле (5) —
◦
θ
=
N
−
1
N
X
i
=1
◦
θ
i
, а
ε
˜
θ
= ˜
θ
−
θ
— оценкам по формуле (6) —
˜
θ
= (
N
0
)
−
1
N
0
X
i
=1
◦
θ
i
−
W
i
. Величины
W
i
=
−
σ
2
r
00
θθ
(
X
i
, θ
)
2 (
r
0
θ
(
X
i
, θ
))
3
, завися-
щие от оцениваемого параметра
θ
, были заменены их приближенными
значениями
f
W
i
=
−
σ
2
r
00
θθ
X
i
,
◦
ˉ
θ
2
r
0
θ
X
i
,
◦
ˉ
θ
3
.
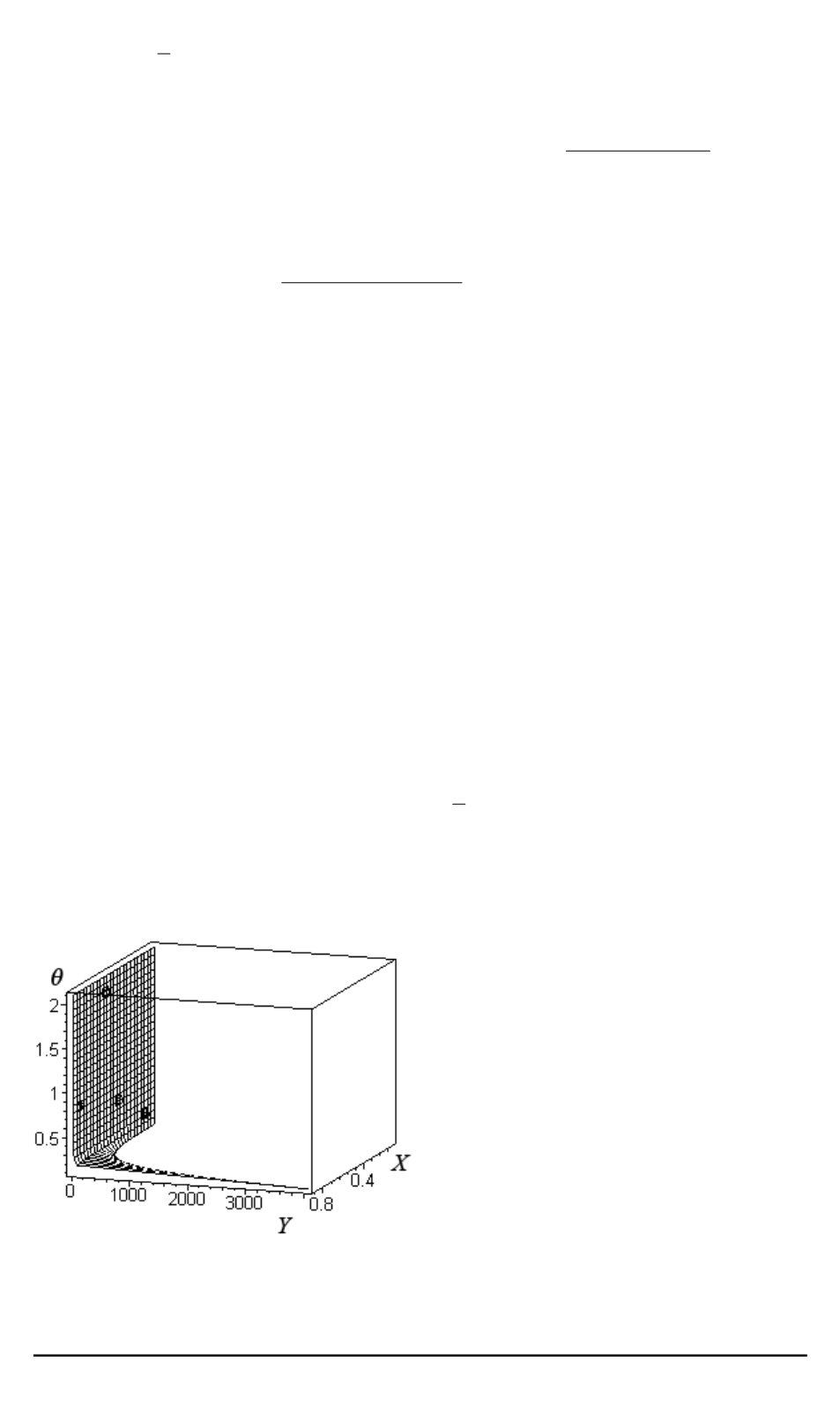
Подробнее остановимся на результатах пятого эксперимента, мо-
дель которого приведена на рис. 1. На рис. 2 изображена поверхность
θ
(
X, Y
)
неявно заданная уравнением
Y
=
r
(
X, θ
)
. Как видно из рис. 2,
в точках с координатами
(0
,
3285
,
0
,
8149)
,
(0
,
7142
,
1
,
0465)
уравнение
θ
=
θ
(
X, Y
)
в области предполагаемых значений
θ
= (0
,
1
,
2)
решений
не имеет. Поэтому
N
=
n
−
2 = 13
. Значение в ячейке
N
0
=
N
−
4 = 9
,
так как четыре точки с координатами
(0
,
2
,
1
.
2646)
,
(0
,
4571
,
1
,
2908)
,
(0
,
5857
,
1
,
0466)
,
(0
,
8428
,
1
,
6071)
были удалены по признаку невы-
полнения условий
теоремы 1
, а именно:
W
i
для них были равны
32,9426; 1,1597; 1,4169; 0,0891, что значительно превышает не только
ε
2
i
≈
σ
2
= 0
,
0408
, но и
ε
i
≈
σ
= 0
,
202
.
Из результатов оценивания, приведенных в таблице, видно, что
при увеличении
N
0
6
N
прослеживается неустойчивая сходимость к
истинному значению
θ
состоятельной оценки
˜
θ
. При этом она является
более точной, чем смещенная оценка
◦
θ
.
Выводы.
1. Предложенная оценка регрессионного коэффициента
однофакторной однопараметрической регрессии, ввиду доказанной ее
Рис. 2. Поверхность
θ
=
θ
(
X, Y
)
, задан-
ная уравнением
Y
=
r
(
X, θ
)
состоятельности, может слу-
жить не только начальным при-
ближением существующих ите-
рационных методов оценивания,
но и быть при некоторых усло-
виях самостоятельной оценкой.
2. В процессе доказательства
состоятельности оценки получе-
ны ее основные характеристи-
ки, а именно: математическое
ожидание и дисперсия, с помо-
щью которых возможно постро-
ение интервальных оценок раз-
личной степени надежности.
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 3


