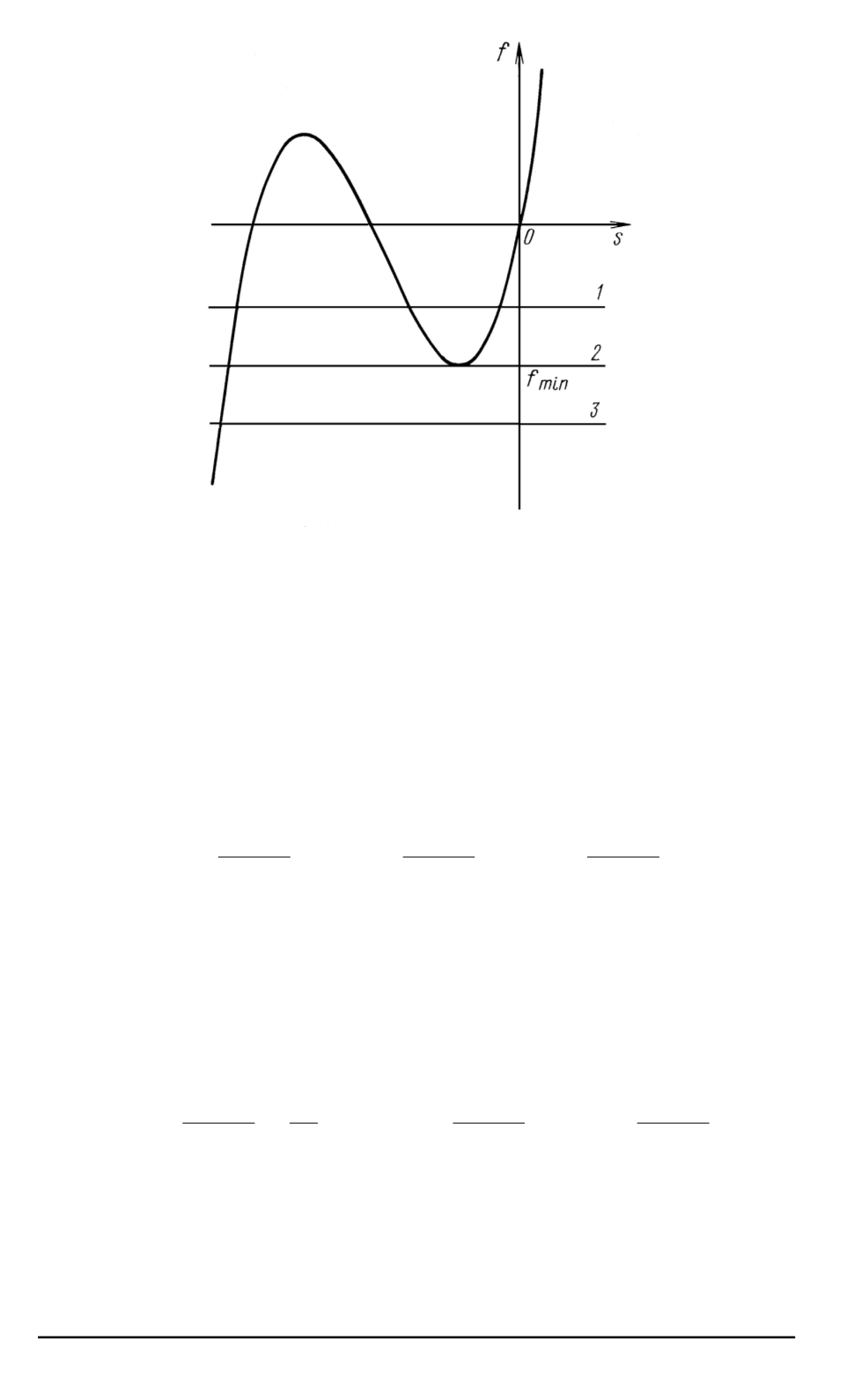
Рис
. 2.
Относительные положения графика многочлена
f
(
s
)
и прямой
f
=
−
BD
для трех случаев
:
1
—
три точки пересечения
;
2
—
одна точка пересечения и одна точка касания
;
3
—
одна точка пересечения
Возможны следующие случаи
.
Первый случай
—
0
>
−
BD > f
min
.
В этом случае уравнение
(7)
имеет три различных действительных корня
s
2
< s
1
< s
0
<
0
,
y
0
(
t
) = exp(
s
0
t
)
, y
1
(
t
) = exp(
s
1
t
)
, y
2
(
t
) = exp(
s
2
t
)
,
y
(
t
) =
C
0
E
+
s
0
D
y
0
(
t
) +
C
1
E
+
s
1
D
y
1
(
t
) +
C
2
E
+
s
2
D
y
2
(
t
)
.
Второй случай
—
0
>
−
BD
=
f
min
.
В этом случае уравнение
(7)
имеет два различных действительных корня
s
2
< s
1
<
0
,
один из кото
-
рых
s
2
(
б
´o
льший по модулю
) —
простой
,
а другой корень
s
1
—
кратный
двум
,
y
0
(
t
) = exp(
s
1
t
)
, y
1
(
t
) = exp(
s
1
t
)
t, y
2
(
t
) = exp(
s
2
t
)
,
y
(
t
) =
µ
C
0
E
+
s
1
D
+
C
1
D
¶
y
0
(
t
) +
C
1
E
+
s
1
D
y
1
(
t
) +
C
2
E
+
s
2
D
y
2
(
t
)
.
Третий случай
—
0
> f
min
>
−
BD
.
В этом случае уравнение
(7)
имеет один действительный корень
s
0
<
0
и два комплексных сопря
-
женных корня
s
1
=
v
+
iw, s
2
=
v
−
iw,
y
0
(
t
) = exp(
s
0
t
)
, y
1
(
t
) = exp(
vt
) cos(
wt
)
, y
2
(
t
) = exp(
vt
) sin(
wt
)
,
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
3
15


