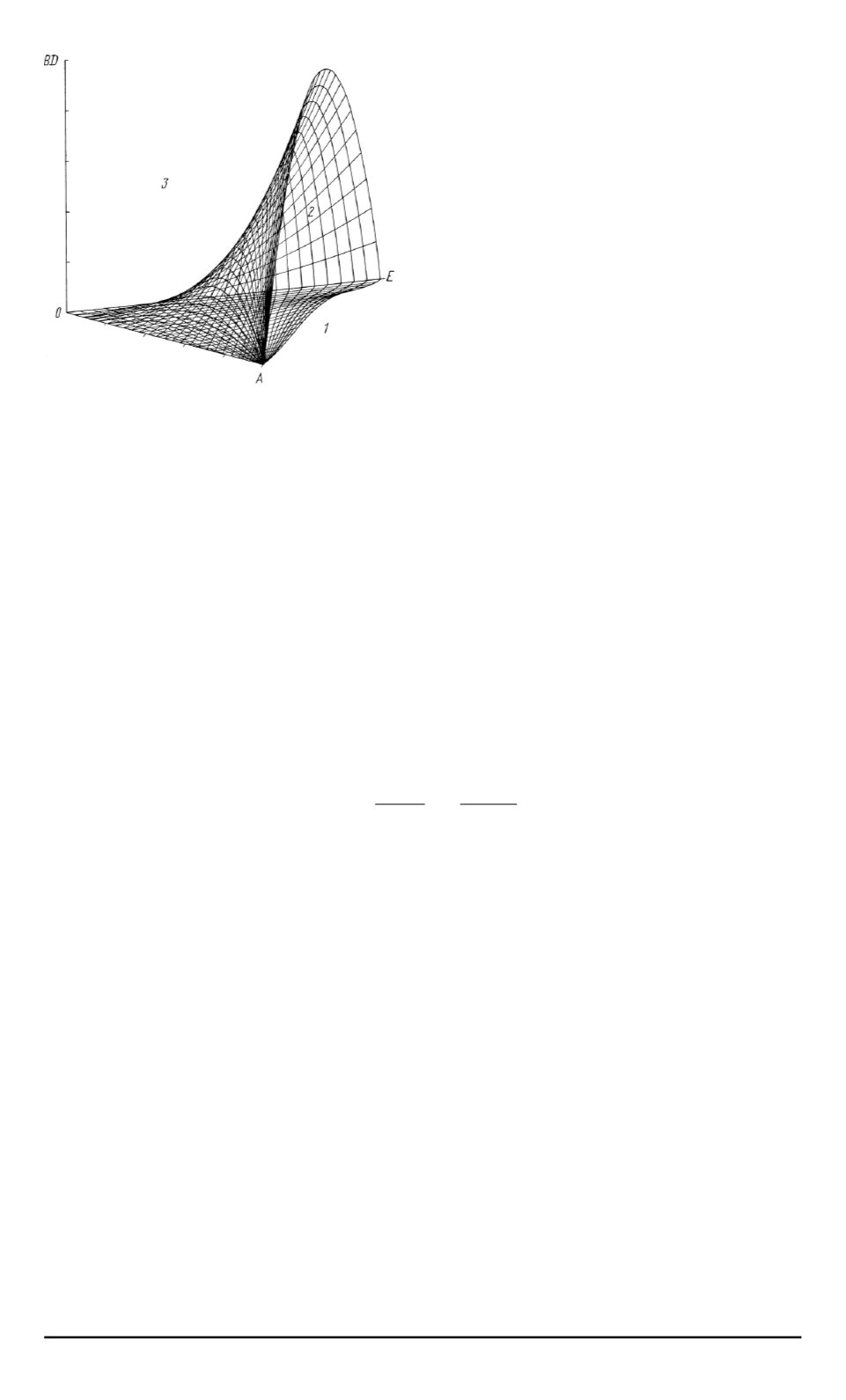
Рис
. 3.
Области устойчивости систе
-
мы автоматического регулирования
угла схождения
:
1
—
область устойчивости
:
экспо
-
ненциальный характер стабилизации
;
2
—
область устойчивости
:
колебатель
-
ный характер стабилизации
(
v <
0)
;
3
—
область расходимости процесса
регулирования
(
v
≥
0)
Если
v <
0
,
то при
t
→
+
∞
функции
y
к
(
t
)
и
y
(
t
)
в этом случае
также являются бесконечно малы
-
ми
,
а система автоматического ре
-
гулирования угла схождения устой
-
чива
(
отметим
,
что
Q >
0
, s
0
< v
).
Если же
v
>
0
,
то амплитуда ко
-
лебаний стремится либо к некото
-
рому положительному числу
(
при
v
= 0
),
либо к плюс
-
бесконечности
(
при
v >
0
).
Отметим
,
что неравенство
v <
0
равносильно неравенству
BD < AE
(
A
+
E
)
.
Зоны устойчи
-
вости системы автоматического ре
-
гулирования угла схождения пред
-
ставлены на рис
. 3 (
в координатах
A
,
E
,
BD
).
В заключение отметим
,
что про
-
веденный анализ позволяет наилучшим образом подобрать значения
параметров при конструировании системы автоматического регулиро
-
вания угла схождения
.
Неравенство
BD < AE
(
A
+
E
)
,
определяющее
устойчивость системы автоматического регулирования
,
равносильно
неравенству
v
а
>
n
1
n
2
kn
2
3
−
k
n
3
m
п
.
(8)
Если правая часть неравенства
(8)
отрицательна или равна нулю
,
то
система регулирования устойчива при любой скорости движения авто
-
мобиля
v
а
.
Если же правая часть неравенства
(8)
положительна
,
то ско
-
рость движения автомобиля должна удовлетворять этому неравенству
.
Таким образом
,
при конструировании системы автоматического регу
-
лирования угла схождения необходимо достигать неположительности
правой части неравенства
(8) (
например
,
уменьшая величины
n
1
, n
2
, m
п
или увеличивая величину
k
).
Если же это невозможно
,
то систему сле
-
дует использовать
,
если скорость автомобиля
v
а
удовлетворяет нера
-
венству
(8).
СПИСОК ЛИТЕРАТУРЫ
1.
Р я з а н ц е в В
.
И
.,
К о п а е в А
.
В
.
Математическая модель системы автоматиче
-
ского регулирования угла схождения управляемых колес автомобиля
//
Вестник
машиностроения
. – 2001. –
№
7. –
С
. 14–18.
18
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2004.
№
3


