Теорема
4
.
Предельное распределение статистики
3
√
nT
1
n
являет
-
ся стандартным распределением Колмогорова
–
Смирнова
:
lim
P
(
3
√
nT
1
n
<
h
) =
P
(
sup
|
R
1
(
t
)
|
<
h
) =
1
−
2
∞
∑
k
=
1
exp
(
−
2
k
2
h
2
)
,
где
R
1
(
t
)
—
нормальный случайный процесс с
ER
1
(
t
) =
0,
ER
1
(
s
)
R
1
(
t
) =
=
s
2
(
3
−
2
s
)
(
1
−
s
)
3
+
s
2
(
3
−
2
s
)
(
1
−
t
)
3
(
1
−
t
)
3
+
t
2
(
3
−
2
t
)
, 0
6
s
6
t
6
1.
Результаты моделирования
.
Для проверки эффективности приме
-
нения статистики
T
2
n
при оценке функций связи
ξ
0
=
ϕ
(
ξ
∗
)
был ис
-
пользован метод Монте
-
Карло
.
Оценивался коэффициент ускорения
k
в функции связи
ξ
0
=
k
ξ
∗
.
Моделировались
n
пар
(
ξ
i
1
,
ξ
i
2
)
одинаково рас
-
пределенных случайных величин
,
по которым вычислялись
n
векторов
(
θ
i
,
γ
i
) ,
где
θ
i
=
min
(
ξ
i
1
,
ξ
i
2
)
,
γ
i
= (
max
(
ξ
i
1
,
ξ
i
2
)
−
min
(
ξ
i
1
,
ξ
i
2
))
/
k
0
,
k
0
—
за
-
данное число
.
Случайные величины
ξ
i
j
моделировались по экспонен
-
циальному закону с параметром
λ
=
10
−
4
.
Эксперимент предусматри
-
вал возможность цензурирования испытаний временем
δ
(
r
)
—
r
-
й по
-
рядковой статистикой из
δ
i
=
θ
i
+
γ
i
,
i
=
1
,
2
, . . . ,
n
.
Величины
δ
i
—
это
общая длительность испытаний
i
-
й пары
.
По этим данным оценивал
-
ся коэффициент ускорения
k
по формуле
b
k
=
argmin
T
2
n
(
k
)
.
При
r
<
n
значения статистики
T
2
n
(
k
)
вычислялись в промежутке
0
6
t
6
δ
(
r
)
.
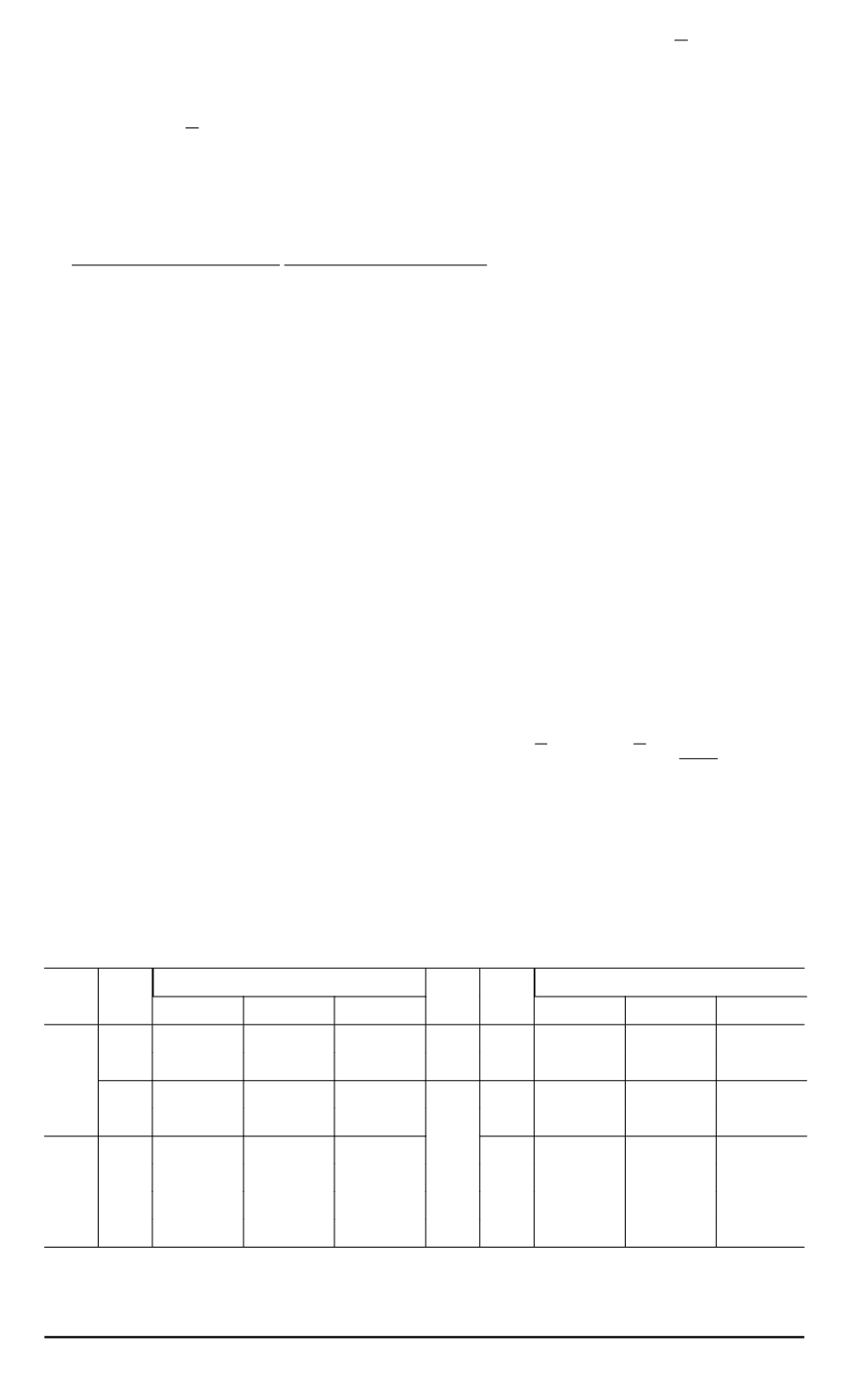
В
таблице приведены значения отношения
ρ
=
k
/
k
0
,
где
k
=
1
500
n
∑
i
=
1
b
k
i
—
среднее по пятистам реализациям оценок
b
k
для каждого набора
(
n
,
r
)
.
Анализ результатов моделирования показал
,
что при
n
>
20
оценка
b
k
имеет незначительное положительное смещение
,
которое постепенно
уменьшается при увеличении
r
.
n r
Значения
k
0
n r
Значения
k
0
3
4
5
3
4
5
20 15 1,1313 1,1312 1,0912 44 42 1,0491 1,0261 1,0388
17 1,0950 1,1285 1,0921
44 1,0390 1,0249 1,0286
19 1,0982 1,1419 1,0987 48 36 1,0594 1,0705 1,0503
20 1,1097 1,1097 1,0820
39 1,0577 1,0288 1,0794
24 18 1,1030 1,1249 1,0820
41 1,0343 1,0523 1,0343
20 1,0837 1,1545 1,1089
43 1,0030 1,0472 1,0374
22 1,0740 1,0900 1,0811
45 1,0645 1,0220 1,0440
24 1,0462 1,0589 1,0367
48 1,0266 1,0073 1,0040
40 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2003.
№
2


